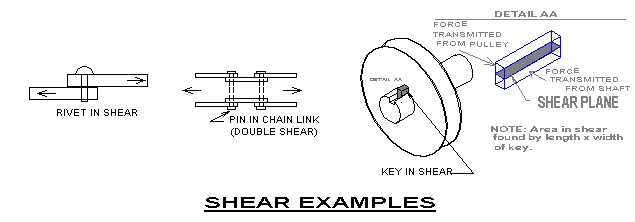
Shear Stress: Shear describes
the condition when parallel forces (planes) occur in opposing directions
such as scissors cutting paper, or a hole punch producing a sheared hole.
Shear strength is also important in mechanical fasteners, power transmission
couples, and manufacturing processes such as punching.
Shear stress is the applied force divided by the area in shear.
Lets look at some practical applications of how shear
stress occurs.
EXAMPLE PROBLEMS:
1. The Rivet shown in the diagram above is
1/4 inch in diameter and subjected to a 500 lb. load. Find the shear
stress in the steel rivet.
S = F / A(shear)
A = .7854 x (.25 in.)2 = .049 in.2
S = 500 lbs. / .049 in.2
= 10,204 psi
2. If the chain link shown in the
diagram is subjected to a load of 1000 lbs, and stress must be limited
to 25,000 psi. What should be the minimum diameter of the pin?
A(shear) = F / S ; = 1000
lbs. / (25,000 lbs. / in.2 ) = .04 in.2
Note: The required total area in shear
is .04 square inches. Since the pin is in double shear, there are
two shear planes. Therefore the cross-sectional area of the pin is
half the calculated area in shear or .02 square inches.
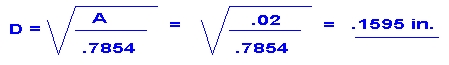
3. Find the shear stress in the key show in the above diagram
if the shaft diameter is one inch and the torque is 1200 lb-in. The
key dimensions are .125 inch wide and 1 inch long.
As= w x L (of key) = .125 in x 1 in = .125 in2
T = F x d (Where d is the radius of the shaft); so F = T /
d
F = 1200 lb-in / .5 in = 2400 lbs.
S = F / As = 2400 lbs. / .125 in2 =
19,200 psi
BACK
HOME
NEXT