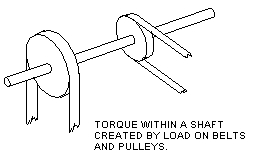
EXAMPLES OF APPLIED TORQUE EXAMPLE PROBLEM: If 50 lb. force is applied to the handle of a 12 inch open-end wrench, how much stress is created in a 1/2 inch bolt?
Solution: S = T / ZP;
T = Force x Distance = 50 lb. x 12 in. = 600 lb-in.
ZP (for solid shafts) = pi x D3 / 16; = (3.1416 x .53)/16
S = 600 lb-in / .0245 in3 = 24,490 psiBACK HOME NEXT