A Simple Model for Estimating Newbuilding Costs

Thanks are due to Harry Benford, Ian L. Buxton, Charles R. Cushing, Kevin Moak, and an anonymous referee, for helpful comments and suggestions. The author retains responsibility for errors or shortcomings.

Abstract

This paper presents a simple model for estimating newbuilding costs. Regression equations are estimated on a large dataset of recent 2003-2007 shipyard deliveries reported in Lloyd's Shipping Economist. The equations developed in this paper can be used in a wide variety of economic analyses involving new ship construction and operating costs. The models presented here capture the most modern design and construction techniques, and most up-to-date cost information, compared to those previously described in the literature.

Key words: newbuilding costs; pooled data; modern ship designs; regression analysis.

Introduction

The established methodology for estimating ship construction and operating costs is largely based on 1960s design- and construction data. Given design dimensions, cargo capacity is determined along with the required amount of steel. The earlier approaches assume steel constructions and are less applicable to some of the more exotic modern materials such as aluminum or composites. They also assume a displacement hull, which is increasingly less valid for newer, higher-speed ships (Baird, 2004; Becker, Burgess and Henstra, 2004). The amount of steel in turn determines the material and labor costs.

The basic approach remains valid, but must be updated in light of modern construction and design techniques which were never captured in the original data. Contemporary ship designs, for example, are routinely optimized by computer with finite element methods to balance minimum fabrication cost and maximum cargo capacity requiring a boxier, more rectangular hull, with minimum drag and maximum fuel economy requiring a more streamlined design. The need for a revised cost estimation methodology becomes increasingly critical as environmental imperatives make waterborne transport the mode of choice (Mulligan and Lombardo, 2006).

Literature Review

The accepted method for estimating ship construction and operating costs is due to Harry Benford, a professor of naval architecture and marine engineering at the University of Michigan, and dates from the 1960s. Benford conducted regression studies with a variety of technical and cost parameters to arrive at basic algebraic relationships among cargo capacity, ship dimensions, degree of streamlining (block coefficient), design operating speed, Admiralty coefficient, required shaft horsepower, required engine size, and ship steel weight. His approach however is based on design assumptions which have grown increasingly less applicable (Benford, 1993).

Benford also estimated relationships between steel weight and labor requirements. This enabled him to estimate separate equations for materials and labor costs to build a cargo ship. Again, both technical design parameters and economic factors have changed so dramatically in the intervening forty years that, at the very least, Benford's equations need to be re-estimated with more modern data.

Benford published his regression studies in two research monographs (Benford, 1961; 1965) and a refereed article (Benford, 1967). Little or no work has been done in this field since then (except Benford, 1991a; 1991b) and his articles, though outdated, remain definitive. Benford's estimates and approach continue to be highlighted in contemporary textbooks (e.g., Hunt and Butman, 1995), due in part to the broad applicability of his approach.

[Table 1 about here.]

Data

Data on newbuilding costs are from Lloyd's Shipping Economist, published from market reports in each monthly issue, for various types and standard ship sizes. For dry bulk carriers, newbuilding prices are given for handysize (45,000 dwt), handymax (51,000 dwt), Panamax (72,000 dwt), and Capesize (170,000 dwt) ships. Tanker newbuilding prices are listed for handymax (clean) (45,000 dwt), Panamax (72,000 dwt), Aframax (110,000 dwt), Suezmax (160,000 dwt), and very large crude carriers (VLCCs) (300,000 dwt). Newbuilding costs are listed for 140,000 m³ liquid natural gas (LNG) tankers up to December 2004 and for 150,000 m³ LNG tankers afterwards. Newbuilding costs are reported for 8,000 m³, 24,000 m³, 52,000 m³, and 72,000 m³ liquid petroleum gas (LPG) tankers. In December 2004, the largest class of LPG tankers, for which data were reported, increased to 78,000 m³. For container carriers, newbuilding prices are given for 1,000 teu, 2,500 teu, 4,000 teu, and 7,000 teu capacities. Starting in May 2005, the largest class of containership in the dataset was increased to 8,000 teu. Newbuilding costs are also given for general cargo carriers of 10,000 dwt and 20,000 dwt. Although some data are available for RoRo and reefer ships, newbuilding costs were not given for these types. Ship sizes by type are summarized in Table 1. To allow for adjustments for inflation, the producer price index (PPI) for heavy industry was taken from the Federal Reserve Bank of St. Louis's Federal Reserve Economic Data website.

Methodology

The dataset includes only two monthly observations for each size and type of ship: newbuilding cost, which is an average of all newbuilding costs of all ships of that type and approximate size delivered in that month, and the standard size category, characterized by deadweight tonnage. Because the data are reported for particular months, cost indices can be used to reflect supply (producer price index) and demand (consumer price index) determinants. The consumer price index was never found to contribute significant explanatory power. This may result from collinearity with the producer price index, or from temporal demand instabilities which, as Dikos (2004) showed, could occur in competitive markets. Although the dataset is unfortunately parsimonious, the number of datapoints included is much greater than Benford (1961, 1965, 1967) was able to include in his otherwise much richer datasets. It is hoped that the larger dataset will allow for more reliable estimates.

With two basic explanatory variables, deadweight tonnage and producer price index, and one thousand observations, it was simple to include second and third order terms in the explanatory variables to explore the possibility of non-linear relationships of the kind successfully estimated by Ådland and Koekebakker (2004, 2007) for secondhand bulk carriers. As newbuilding costs were reported in current dollars, i.e. not adjusted for inflation, one approach could have been to adjust for inflation by a price index before estimation. However, with a view toward the final user who would need to predict newbuilding costs in current-year rather than base-year dollars, the price indices were included in the basic specification.

The general specification was modeled as a first-order function of the PPI and a third-order function of deadweight tonnage:

Newbuilt Cost = a(PPI) + b(dwt) + c(dwt)² + d(dwt)³

Four dummy variables were added to this basic specification to distinguish among observations for five different type ships as described above. Statistically insignificant coefficients were then deleted from the model to arrive at a final specification.

Results

The first approach is to pool the dataset including all dissimilar ship types. Estimation of a single model including all ship types allows available degrees of freedom afforded by the large dataset to be used to the fullest advantage. Each type is distinguished in the dataset by dummy variables for each type: dry bulk carriers, containerships, tankers, liquid petroleum gas tankers, and liquid natural gas tankers. General cargo ships are also included in the dataset and are distinguished from other types by the absence of a dummy set to one for that type. Omitting the dummy for one category is a standard and necessary practice to avoid a non-invertible, exactly-singular matrix which would make it impossible to estimate regression coefficients. The other variables in each observation are the newbuilding cost in current dollars, the producer price index, and the deadweight volume for each ship, and its square- and cubic power.

With 1,000 observations and ten estimated coefficients (an intercept, coefficients on four ship type dummies, and coefficients on the producer price indexPPI, dwt, dwt², and dwt³), the estimate's degrees of freedom were 990. An alternative approach would have been to suppress the intercept to reflect the fact that the ship estimate model R: this is shipbuilding cost and not ship model should pass through the origin so that a ship of zero size should cost zero dollars. This approach was dropped because the dummy variables estimate independent, non-zero, intercepts for each ship type anyway.

[Table 2 about here.]

The pooled regression is reported in Table 2. T-statistics are significant for all variables in this specification. The coefficient of PPI is positive and significant. More explicitly, the coefficient value of 2.6 implies an average increase in newbuilding cost of 2.6 million dollars for every one percent increase in the PPI. However obvious this finding may seem, it lends credence to the estimate. The first-order coefficient on deadweight volume indicates that the larger a ship’s tonnage, the more it will cost, which again is a fairly intuitive finding. On average, and across all types of ships, every increase in 1,000 tons deadweight results in an increase of 1.8 million dollars in newbuilding cost. The second-order coefficient of tonnage is negative and significant, indicating that scale economies are present, but the third-order term is positive and significant, indicating scale economies are not unlimited.

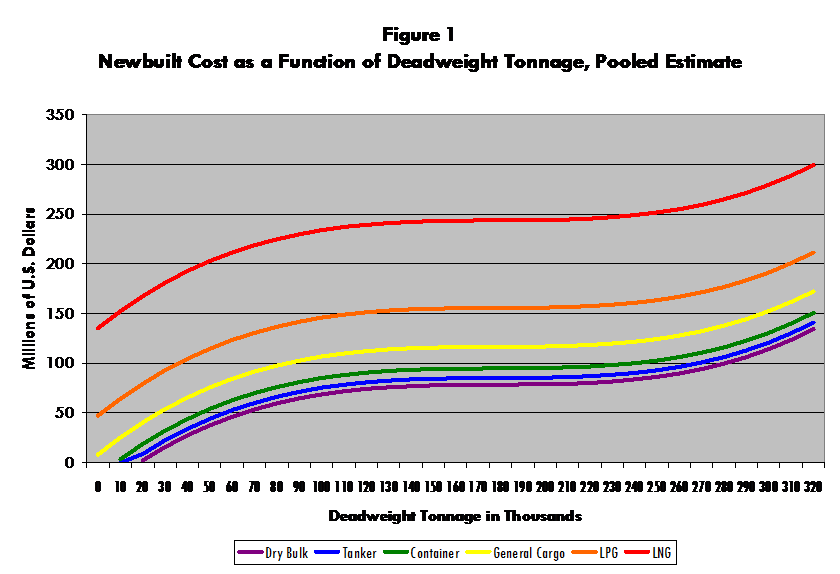
[Figure 1 about here.]

Equations for forecasting newbuilding costs based on this estimate are presented below for liquid natural gas carriers (LNG), liquified petroleum gas carriers (LPG), general cargo carriers (GC), container carriers (C), tankers (T), and dry bulk carriers (B), listed in order of decreasing cost:

C_LNG = - 253.012 + 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

C_LPG = - 341.082 + 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

C_GC = - 380.078 + 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

C_C = - 401.727 + 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

C_T = - 411.551+ 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

C_B = - 418.202 + 2.60(PPI) + 1.8053(dwt) - 0.01009(dwt)² + 0.0000189(dwt)³

The dummy variable coefficients are also all significant and serve to distinguish the different types of ship, which have systematically different costs. LNG tankers are dramatically more expensive than other types of ships. Bulk carriers, tankers, and containerships cost less. Containership cost is not much less than general cargo carriers, though the small difference is statistically significant. LNG tankers are the most expensive ship type; dry bulk carriers the cheapest to build, followed by ordinary tankers. Assuming a fixed PPI = 149.3 (May 2007), newbuilding costs vary with deadweight tonnage as illustrated in Figure 1.

Next, we set the ship type dummy variables aside and estimate separate regression models for each type of ship. The dummy variable approach allows for estimates with more degrees of freedom while estimating independent intercepts, slopes, and algebraic specifications, for each type of ship. Estimating separate regressions makes the slope coefficients independent as well as the intercepts. Separate regression models are reported in Table 3.

[Table 3 about here.]

Interestingly, intercepts are always large and negative, particularly considering that they are dimensioned in millions of dollars. Newbuilding cost always rises directly with size and the price index. Higher-order terms in deadweight tonnage were only significant for dry bulk carriers. Thus, all the other independent estimates yield linear models.

C_LNG = - 885.127 + 5.56(PPI) + 5.3368(dwt)

C_LPG = - 385.921 + 2.86(PPI) + 2.1444(dwt)

C_GC = - 34.903 + 0.304(PPI) + 0.6740(dwt)

C_C = - 219.933 + 1.56(PPI) + 0.5961(dwt)

C_T = - 480.899 + 3.530(PPI) + 0.2611(dwt)

C_B = - 291.147 + 1.689(PPI) + 2.8526(dwt) - 0.03165(dwt)² + 0.00011(dwt)³

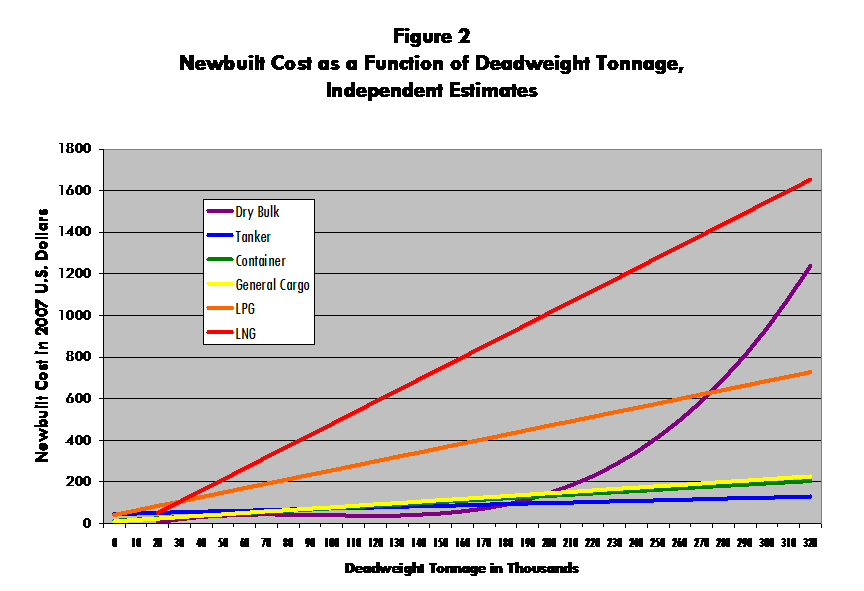
[Figure 2 about here.]

These relationships are graphed in Figure 2. One implausibility of the third-order, nonlinear cost function for dry bulk carriers is that cost declines between about 70,000 and 120,000 tons, suggesting that a linear specification may be preferable.

An Illustration

Given the equations presented above, it will help to illustrate how they might be used by practitioners and shipping analysts. A firm contemplating a building programme needs to have some idea at the preliminary stage of what magnitude of newbuilding costs they may be confronted, before they can employ more sophisticated forms of analysis such as Bendall and Stent's (2005) real option valuation model.

Posit the potential construction of an 8,000 teu, 170,000 ton containership, with contract date of mid 2010 and delivery scheduled for late 2011.The contract date determines the number of years of compounding for the price index. Assuming an inflation rate of three percent, compounded for three years, and starting with the May 2007 PPI of 149.3, the PPI is multiplied by (1.03)³ = 1.0927. This gives 163.1 for the projected 2010 PPI. Together with the desired deadweight tonnage, these parameters are plugged into the newbuilding cost equations, first using the pooled estimate equation from Table 2:

C_C = - 401.727 + 2.60(163.1) + 1.8053(170) - 0.01009(170)² + 0.0000189(170)³

= 130.90 million USD in 2010

Alternatively, using the unpooled estimate from Table 3, a simpler, linear specification yields:

C_C = - 219.933 + 1.56(163.1) + 0.5961(170)

= 136.37 million USD in 2010

Though the two equations accord fairly closely, they can be interpreted as a probable range in which newbuilding costs will likely fall, given contract time, design size, and assumptions about inflation. These estimates depend on projected future PPIs for heavy industry, reflecting both shipyard cost and the level of demand faced by shipyards. Consequently, estimates from these equations can be performed for a variety of projected levels of PPI inflation. These estimates are presented in Table 4 for several different hypothesized inflation rates.

[Table 4 about here.]

Conclusion

This paper presents new models for estimating newbuilding costs, based on recent 2003-2007 data. This dataset reflects contemporary ship design and construction practices, and recent cost trends. The models can be used as a basis for economic analysis whenever newbuilding ship cost is considered as an alternative. Though not making an abrupt break with accepted practice, the cost equations presented above offer various advantages for shipping economists and strategic planners. Estimating newbuilding costs with these models captures recent practical experience and cost trends facing the industry in the past few years.

References

Ådland, ROS and Koekebakker, S (2004). Market efficiency in the second-hand market for bulk ships. Maritime Economics & Logistics 6(1): 1-15.

Ådland, ROS and Koekebakker, S (2007). Ship valuation using cross-sectional sales data: a multivariate non-parametric approach. Maritime Economics & Logistics 9(2): 105-118.

Baird, AJ (2004). Investigating the feasibility of fast sea transport services. Maritime Economics & Logistics 6(3): 252-269.

Becker, JFF; Burgess, A; and Henstra, DA (2004). No need for speed in short sea shipping. Maritime Economics & Logistics 6(3): 236-251.

Bendall, HB and Stent, AF (2005). Ship investment under uncertainty: valuing a real option on the maximum of several strategies. Maritime Economics & Logistics 7(1): 19-35.

Benford, H (1957). Engineering economy in tanker design. Society of Naval Architects and Maritime Engineers Transactions 65: 775-838.

Benford, H (1958). Ocean ore-carrier economics and preliminary design. Society of Naval Architects and Maritime Engineers Transactions 66: 384-442.

Benford, H (1961). Status of research into engineering economy in the design of general cargo ships. Ann Arbor, Michigan: University of Michigan.

Benford, H ([1962] 1965). General cargo ship economics and design. Ann Arbor, Michigan: University of Michigan.

Benford, H (1963). Principles of engineering economy. Society of Naval Architects and Maritime Engineers Transactions 71: 387-424.

Benford, H (1967). The practical application of economics of merchant ship design. Marine Technology, Society of Naval Architects and Marine Engineers (January).

Benford, H (1991a). A naval architect's guide to practical economics. Report No. 319. Ann Arbor: Department of Naval Architecture and Marine Engineering, University of Michigan.

Benford, H (1991b). Naval architecture for non-naval architects. Jersey City, New Jersey: Society of Naval Architects and Marine Engineers.

Benford, H (ed.) (1993). A half-century of maritime technology. Jersey City, New Jersey: Society of Naval Architects and Marine Engineers.

Benford, H; Thornton, KC; and Williams, EB (1962). Current trends in the design of iron-ore ships. Society of Naval Architects and Maritime Engineers Transactions 70: 24-83.

Dikos, G (2004). New building prices: demand inelastic or perfectly competitive? Maritime Economics & Logistics 6(4): 312-321.

Federal Reserve Bank of St. Louis (2007). Federal Reserve Economic Data. http://research.stlouisfed.org/fred2/.

Hunt, EC and Butman, BS (1995). Marine engineering economics and cost analysis. Centreville, Maryland: Cornell Maritime Press.

Lloyd's Shipping Economist (various issues). London: Lloyd's Marine Intelligence Unit, Informa UK, Ltd. Websites http://www.shipecon.com & http://lloydsmiu.com.

Mulligan, RF and Lombardo, GA (2006). Short sea shipping: alleviating the environmental impact of economic growth. World Maritime University Journal of Maritime Affairs 5(2): 55-70.

Table 1 Standard Ship Sizes Included in the Dataset
Dry Bulk Carrier	Handysize	45,000 dwt
	Handymax	51,000 dwt
	Panamax	72,000 dwt
	Capesize	170,000 dwt
Tanker	Handymax (clean)	45,000 dwt
	Panamax	72,000 dwt
	Aframax	110,000 dwt
	Suezmax	160,000 dwt
	VLCC	300,000 dwt
LNG Tanker	140,000 m^3	49,500 dwt
	150,000 m^3	53,000 dwt
LPG Tanker	8,000 m^3	2,800 dwt
	24,000 m^3	8,500 dwt
	52,000 m^3	18,000 dwt
	72,000 m^3	25,000 dwt
	78,000 m^3	27,500 dwt
Container Carrier	1,000 teu	45,000 dwt
	2,500 teu	51,000 dwt
	4,000 teu	72,000 dwt
	7,000 teu	150,000 dwt
	8,000 teu	170,000 dwt
General Cargo	10,000 dwt	10,000 dwt
	20,000 dwt	20,000 dwt
Source: Lloyd's Shipping Economist, various 2003-2008 issues.

Table 2 Newbuilding Cost Model I: Ship Type Distinguished by Dummy Variables
Pooled Data	Coefficient	Std Error	t-statistic	Probability
Intercept	-380.07788	15.2686	-24.8927	0.00000
LNG	127.06628	2.4552	51.7540	0.00000
LPG	38.99597	1.3126	29.7087	0.00000
Containership	-21.64896	2.1654	-9.9976	0.00000
Tanker	-31.47307	2.3069	-13.6428	0.00000
Dry Bulk Carrier	-38.12387	2.1339	-17.8657	0.00000
PPI	2.60120	0.1056	24.6404	0.00000
DWT	1.80527	0.0760	23.7634	0.00000
DWT^2	-0.01009	0.0006	-18.1144	0.00000
DWT^3	0.0000189	0.0000	16.6142	0.00000
No Obs	1000		Adj R^2	0.9311032

Table 3 Newbuilt Cost Models, Various Type Ships, Independent Estimates
1. LNG Tanker	Coefficient	Std Error	t-statistic	Probability
Intercept	-885.12736	33.26143	-26.61122	0.00000
PPI	5.56042	0.43918	12.66095	0.00000
DWT	5.33685	0.81423	6.55445	0.00000
No Obs	50		Adj R^2	0.96846
2. LPG Tanker	Coefficient	Std Error	t-statistic	Probability
Intercept	-385.92095	14.87953	-25.93637	0.00000
PPI	2.86128	0.10340	27.67195	0.00000
DWT	2.14442	0.03649	58.76587	0.00000
No Obs	200		Adj R^2	0.95593
3. General Cargo	Coefficient	Std Error	t-statistic	Probability
Intercept	-34.90298	8.08377	-4.31766	0.00004
PPI	0.30392	0.05603	5.42459	0.00000
DWT	0.67400	0.03589	18.78102	0.00000
No Obs	100		Adj R^2	0.79339
4. Container Carrier	Coefficient	Std Error	t-statistic	Probability
Intercept	-219.93267	32.31667	-6.80555	0.00000
PPI	1.56284	0.22469	6.95559	0.00000
DWT	0.59606	0.01586	37.59086	0.00000
No Obs	200		Adj R^2	0.88182
5. Tanker	Coefficient	Std Error	t-statistic	Probability
Intercept	-480.89908	20.66656	-23.26943	0.00000
PPI	3.52981	0.14347	24.60287	0.00000
DWT	0.26107	0.00510	51.14381	0.00000
No Obs	250		Adj R^2	0.92820
6. Dry Bulk Carrier	Coefficient	Std Error	t-statistic	Probability
Intercept	-291.14668	30.84261	-9.43976	0.00000
PPI	1.68883	0.09013	18.73703	0.00000
DWT	2.85256	1.14969	2.48116	0.01394
DWT^2	-0.03165	0.01413	-2.24080	0.02617
DWT^3	0.00011	0.00005	2.22859	0.02698
No Obs	200		Adj R^2	0.92121

Table 4 Projected Newbuilt Cost for Hypothetical 170,000 dwt Container Carrier, Contract Date 2010
Projected Inflation rate	Projected 2010 PPI	Pooled Estimate (Table 2)	Unpooled Estimate (Table 3)
3%	163.1	130.90	136.37
4%	167.9	143.38	143.86
5%	172.8	156.10	151.51
6%	177.8	169.07	159.30
Notes: 1. PPI is projected n years into the future assuming a particular annual PPI inflation rate i by the formula PPIt+n = PPIt(1+i)^n. The inflation rate must be represented as a decimal fraction, i.e., 3% = .03. 2. Estimated cost is given in millions of current year (2010) unadjusted U.S. dollars.