College athletic directors face the difficulty of setting a price for goods and services they provide to the public. One complementary good provided as a part of major college sports events is game-day programs. This paper estimates a demand function for football programs using 11 years of data for an NCAA Division I-AA college. Least median of squares (LMS), a new outlier-resistant estimation technique, is used to refine the model and provide a more useful estimate of the demand function. The revenue- and profit-maximizing program price is found and compared with prices actually charged throughout the sample period.

Along with other complementary goods, such as concessions and paraphernalia, game-day programs, rosters, and/or magazines, provide athletic managers an opportunity to capitalize on the captive crowd inside a stadium. Considering the growth in stadium capacities and interest, athletic directors and promotion managers need to understand the increased potential market and factors that influence sales levels to make the most of these changes.

College athletic programs, like commercial firms, pursue goals of profit and revenue maximization. Also like commercial firms, colleges seek to enhance their reputation and consumer awareness. Despite their monopolist position as sellers of concessions and ancillary paraphernalia, they cannot ignore demand, setting an arbitrary price, especially a high one, and expect to maximize revenues or profits. This is especially true in the case of programs, which, unlike food, can be consumed by more than one spectator. A practical demand model and cost estimates would provide information for managers to select a price that achieves their goals.

This paper estimates such a demand function based on 11 years of home game data for a division I-AA collegiate football team[1]. A new outlier-resistant estimation technique, Least Median of Squares (LMS), supplements the traditional Ordinary Least Squares (OLS) to produce a better estimate of the demand model. It unveils the influence of single outlying games or groups of them, allowing practitioners to adapt the model or price for such conditions.

Literature Review

Researchers have studied the demand for athletic events for many years but not the subsequent demand for complementary goods inside the athletic arena (Cairns 1990; Schofield 1983). In the case of football, most of the demand studies investigated professional soccer in Great Britain (Peel & Thomas 1988; Cairns 1987), though there have been a few studies that involved the NFL in the United States (Cebula, Austin, Wildener, & Belton 1997; Welki & Zlatoper 1994; Cairns, Jennet, & Sloan 1986; Siegfried & Hinshaw 1979). Cairns (1990) summarized many of these efforts and categorized the sets of independent variables that researchers generally included to determine the demand in specific instances. These categories included:

Ticket price

2. Income

3. Uncertainty of outcome

4. Importance of outcome for team standing

5. Quality of teams

6. Size of potential audience

7. Weather

8. Broadcast influences

Cairns (1990) discussed problems with measurement of these variables as well as mathematical form. One problem that remains unstudied is the effect of outliers, special games or circumstances that made spectator behavior atypical. Such games can overly influence OLS estimates, unless they suggest other factors to incorporate in the model and account for the influence. This is especially true when there are several outliers under the same influence.

LMS is especially suited to pinpointing such games so researchers and managers can study them for additional information about spectator behavior. Unlike many other outlier-resistant techniques, LMS discovers clusters of outliers that together overly influence estimates, while most other techniques, such as Studentized residuals and DFFITS, only check the influence of one point at a time. Generally, these other techniques fail to recognize groups of outliers, and thus ignore potential information and causal variables that segregate observations into a cluster (Rousseeuw & Leroy 1987; Rousseeuw 1984, 1997).

The Original Model

From an economic standpoint and given the funding goals that pervade most programs, especially at the Division I-AA level, profit maximization or revenue maximization would be useful and not unexpected goals. Secondary goals might include maximizing unit sales to promote long-term allegiance to the team and school, or providing information that broadens or heightens interest in the current and future games along atypical dimensions, such as a specific player’s performance (on and/or off the field), a chance for the league or national title, a new coach with a new style or emphasis, and upcoming events in other sports. The athletic administration decides the price and quantity it expects to sell to achieve these goals.

Simply put, demand for programs (Q) depends on their price (P) and the potential market measured by game attendance (A). Program consumption behavior is different at certain games than at others, so dummy variables are added. F = 1 for the first game of a season. The first game of the new season represents a special sales opportunity when uncertainty about the team and individual players is high and interest in football is renewed rather than routine, as it would be later in the season. H = 1 for homecoming, another special interest game. Our assumptions imply demand adheres to the following functional form:

(1) Q = f(P, A, F, H)

Complexity derives from the demand for the game, A, which is influenced by the variables mentioned by Cairns (1990) in the literature review.[2]

(2) A = f(RSP, I, U, IMP, QUAL, S, W)

where RSP = reserved seat price[3]

I = income

U = uncertainty of outcome

IMP = importance of outcome to teams

QUAL = quality of teams

S = size of potential audience

W = weather condition variables

Consequently, substituting equation (2) into equation (1), the reduced form function for program demand is:

(3) Q = f(P, F, H, RSP, I, U, IMP, QUAL, S, W).

Here, some independent variables are expressed as general categories to be further delineated in the data section that follows, namely U, IMP, QUAL, S, and W.

The program sales total revenue function is the product of equation (3) and P. From the total revenue function, optimization techniques should produce the price and quantity that would maximize revenue from program sales. Using a marginal cost value provided by the administration, the approximate price and quantity to maximize profit results. Traditional statistical techniques are used to evaluate the model. As mentioned earlier, the LMS technique is employed to determine the influence of outliers and discover additional factors that influenced demand. In addition, we use a sample of more recent games to evaluate the precision of the model.

Two kinds of capacity constraints are present in this context. One is imposed by the print run negotiated before the season starts. Demand and attendance forecasts inform this decision. The second constraint is imposed by the venue, which physically limits attendance, limiting in turn the maximum possible program sales. However, neither constraint is relevant in this particular case because ticket-sellout and program-sellout games are omitted from the data set.

Data

To operationalize the general expression (3) so we can estimate the model for program sales, we must measure the general factors, such as importance of the game, mentioned earlier (U, IMP, QUAL, S, and W). To arrive at a practical formulation for all the variables, summarized below as equation (4), we explain our breakdown of these variables and the data.

Three variables, P, RSP, and T, measure the cost of attending the game and purchasing the program. Both prices are expressed in real terms (1982-1984 is the base year). A nominal price that changes each year but remains constant over each season might well pick up all season-to-season variation, not just price effects. However, the nominal price seldom changed during the time span of this study. Furthermore, because we deflated the price variable by the monthly CPI, the inflation-adjusted price variable changes monthly rather than by season. More formal seasonal adjustment would be problematic due to the relatively short college football season. Mapquest supplies T, travel time between the opponent’s and home-team’s locations, an element of trip cost (Siegfried & Eisenberg 1980). Another basic factor, income (I), also influences demand.

Measuring uncertainty is itself an uncertain process (Siegfried & Hinshaw 1979). A ratio of win records reflects the uncertainty (U) of the outcome in this model. The winning percentage of the team with the poorest record is always in the numerator and the better win percentage is the denominator. Consequently, U ranges between 0 and 1. Game outcome is generally more uncertain the larger the U value because teams with identical records yield a value of one.[4]

Following earlier work, the impact of team quality and game importance on attendance is considered (Siegfried & Hinshaw 1979; Rottenberg 1956). The individual quality of the teams draws spectators excited by the chance to see a good team. Individual win percentages for the home team (W) and for opponents (WO) measure these aspects of attendance that flow into the program purchase decision. Because the home team seldom figured in championships at any level, though some opponents did, this variable reflects the importance of the outcome. A team usually struggles to attain the best record possible, and a better win record motivates continued spectator interest. This vector of home and visitor win percentages is cumulative for the current season, except when first home game is the season opener, when the previous season’s win percentage is used.

A vector of current enrollments at the home team’s university (E) and at the opponent’s (EO) represents potential market size. These also proxy alumni base. Siegfried & Eisenberg (1980) discuss alternative measures of market size. The vector (T for game-time temperature, R for rain) reflects the weather. Siegfried & Hinshaw (1979) discuss the impact of rain on attendance. Dummy variables (F) and (H) represent the first home game of the season and the annual homecoming game.

Together, these refinements imply the following detailed reformulation of equation (3):

(4) Q = f(P, RSP, T, I, U, W, WO, E, EO, TMP, R, F, H)

The empirical section presents estimates of this reduced form equation. Table 1 lists the variable definitions and descriptive statistics. The data is on a per game basis for home games played during the 1989 through 1999 seasons for a total of 56 games. Games where programs sold out are omitted. Table 2 provides a correlation matrix.

Estimation Techniques

First, we estimate the model with ordinary least squares (OLS). OLS models minimize the sum of squared residuals. However, squaring values inflates or weights each value by itself. Extreme values or outliers receive especially heavy influence in the process. Accordingly, OLS shifts the line to accommodate these outliers and reduce their residuals. This process distorts estimated coefficients. Consequently, OLS often masks outliers with smaller residuals than they deserve. In the process OLS hides information from analysts, most notably the undistorted estimate revealed by typical data as well as unacknowledged factors, such as games against particular teams, that influence program sales.

Next, to counteract this OLS shortcoming and improve on the OLS estimates, least median of squares (LMS), an outlier-resistant technique, is employed. This technique identifies outliers by producing a set of coefficient estimates that minimizes the median of the squared errors produced by these coefficients. To determine if the outliers provide further information about program sales, we search for their common traits or causes. This step suggests additional factors to include in the model estimated with all available data, which subsequently reduces the OLS objective function.

The structural program demand function (Equation 1) is estimated by OLS, two-stage least-squares (TSLS), and block-recursive estimation in Table 3. Two-stage estimates display low R-squares, and more troubling, positive coefficients on both ticket and program price. Because the estimates go against economic intuition, they cannot support managerial decision making. Indeed, positive coefficients on program price suggest managers who want to increase program sales should increase program price. Such counter-intuitive results could be due to problems such as multicollinearity, errors in data measurement, omission of one or more important independent variables, or some other form of specification error. Since White specification tests on the reduced form equation indicate no statistically significant specification error in the reduced form (see Table 4), it should be recalled that in general, a reduced form may be mathematically derivable from more than one structural equation. Therefore, it is possible for the structural equations to be incorrectly specified while the reduced form derived from them is correctly specified. Consequently, it is useful for explaining and predicting behavior of the dependent variable. In fact, it is a plausible first approach that adequately illustrates the model and optimization process. The model is parsimonious, passes specification tests, produces good statistical results, and produces results that agree well with expectations and economic theory. Because the reduced form is simpler to estimate, practitioners will probably find it more useful.

We proceed with estimates of the reduced form program demand equation which are used to refine the model and illustrate optimal pricing.

Empirical Findings

OLS Results

OLS estimates of the proposed linear model appear in column 1 of Table 4.[5] All coefficients possess the expected sign, except income (I) and enrollment for the home-team institution (E). Income is a problem because national trends do not necessarily reflect local and regional patterns. In addition, other researchers find mixed and generally little support for income as a factor in attendance (Cairns 1986, p. 15).

Not unexpectedly, the insignificant enrollment coefficient suggests current students are not big program customers. In fact, the coefficient sign indicates their presence reduces sales, but the coefficient is not significantly different form 0 for a one-tail test. Please note that we adjusted the two-tail p-values in Table 4 for one-tail tests. The negative sign on home-institution enrollment is unexpected, and so far inexplicable, but also insignificant in the one-tail test. While the correlation coefficient between P and E, –0.76, is higher than we would like, the standard errors of both variables are sufficiently small to produce T statistics both above 0.05 critical values (though in the wrong direction for E). It seems reasonable to search elsewhere for an explanation for the negative sign. Flooding the student section with program sellers would probably not be the best use of limited sales personnel, because non-student spectators are more likely to have funds to buy. Heightened interest and loyalty, evidenced by their decision to spend funds and travel to the game, in turn, reflects increased likelihood of a program purchase. It is entirely plausible that higher enrollment results in lower program sales as student attendees crowd out these non-students who are more likely to purchase programs.

One-tailed tests suggest that of the three customer cost variables (P, RSP, and T) only program price (P) significantly affects program sales. This coefficient is significant at the 0.05 level, one-tail. Opponents with large win records significantly impact sales (at the 0.01 level, one-tail), while hot days (at the 0.05 level, one-tail) and rain (0.01 level, one-tail) counteract the positive factor. Special games, such as the first home game of the season (0.01 level, one-tail) and homecoming (0.05 level, one-tail), increase sales and offer opportunities for increased revenue and profits.[6]

The estimates provide some promise for understanding program sales but disappoint as well. Although the F is significant (0.01 level), the R² of 57.8% suggests problems in capturing major factors in the sales process. Also one game in the data set produces sales of only 90 programs—a very unusual value compared to all the other sales values (with a mean of 360 and a standard deviation of 21). OLS standardized residuals conceal this problem (count of outliers from standardized residuals shown in Table 4). The shaded cells in Table 5 show the outliers that Studentized residuals and DFITS techniques identify from the OLS model. This OLS model potentially masks aberrant sales values, because they unduly influence OLS to minimize the sum of squared residuals. We employed an alternative estimation technique, LMS, to investigate these possibilities and improve on the mixed evaluation results.

LMS Results

To improve on the original model and incorporate other important factors, we employ least median of squares (LMS), an outlier-resistant technique mentioned earlier. This technique identifies outliers by producing a set of coefficient estimates that minimizes the median of the squared errors produced by these coefficients. Each LMS iteration requires 14 observations from the data set (based on 13 coefficients for explanatory variables and one for the intercept). These observations form a set of equations with 14 unknowns or estimates. LMS sorts the squared residuals that result from each iteration and then locates the median of these values. We present the solution produced from the subset of 14 observations with the smallest median squared error among the sample of subsets attempted. Because of the unusually large number of iterations (subsets) and computer resources required to find the exact solution, the LMS program employs random subsets rather than all possibilities in an attempt to locate this solution (Rousseeuw & Leroy, 1987). We enhance this process by rearranging our data set and starting new searches. The eventual solution subset in this paper identifies 14 statistical outliers (see Table 5).[7]

For comparison purposes (with the eventual rival model in the next section), we report a reweighted least squares estimate (RWLS) in Table 4. We remove the outliers, including the 90-program one mentioned in the last section. Model statistics improve.[8] Three additional coefficients are significant at the 0.01 level (travel time T, home win percentage W, and opponent enrollment EO). Opponent win percentage WO becomes insignificant. Program-buying spectators appear more often when the home team wins.

To determine if the outliers provide further information about program sales, we search for their common traits or causes. This step suggests additional factors to include in the model. While this RWLS model may appear a suitable stopping point in model estimation, it is actually a plateau from which we launch an improved model that incorporates any newly discovered factors.

Information from Outliers and the Rival Model

LMS identified 14 outliers. With those observations dropped from the data set, RWLS estimates provide new and hopefully better insight into the impact of the independent variables on program sales. At this stage of the research process, analysts might consider the RWLS estimate a working model of practical value. To do so may alarm other analysts concerned that information is lost or not incorporated in the result—especially in this case, where 25% of the entire data set drops from the scene. On the other hand, we view this situation as ripe with more information about program sales than either the original OLS or the RWLS model incorporates. Perhaps the fourteen observations stand out from the other 42 for some common reason—perhaps the OLS and RWLS models are misspecified because important factors are excluded from the model.

Studentized residuals and DFITS find more outliers than standardized residuals, because they are based on single elimination of data points. These techniques attempt to avoid the OLS masking problem mentioned earlier. However, because Studentized residuals and DFITS are single-observation techniques, and because OLS potentially masks any remaining extreme points, these techniques identify fewer outliers (shaded cells of Table 5) than LMS. These limits do not affect LMS, so there is greater leverage for identifying variables missing from a model.

No characteristics appear outstanding and uniformly applicable to all or even a majority of these fourteen games. However, games with a nearby conference rival appear five times—more than one-third of the LMS outliers. The rival, Furman, does not stand out in the single-observation techniques as it does with LMS. This team is not the traditional or archrival, but is nearby (about 2.5 hours away) and both it and the home team are perennial conference rivals and were major rivals on the national scene earlier. During the 1989-1999 period, the rival played seven games in the home team’s stadium.[9]

To account for this team’s special effect, we estimate a new OLS model. It includes a dummy variable for games against this particular rival.[10] This model does locate the 90-program sales value as an outlier. The rival effect is statistically and practically significant. Expected program sales rise by 135 programs for games with this rival compared to other games where the other variable values are identical. Mean sales without the rival are 340 programs, so 135 programs represents a 40% increase over expectations for games against other opponents.

Ramsey's (1969) RESET test fails to reject the null hypothesis of no specification error, suggesting all variables should be retained in the model. Most coefficient test results remain the same as for the first OLS model, but the home-team’s win percentage, W, is now close to significance at the 0.05 level (actually at the 0.065), one-tail. The coefficient on the dummy variable indicating the rival is significant at the 0.05 level, one-tail.

From the model, we can generally conclude that one real-dollar increase in program price (about $1.73 currently) will diminish sales by 354 programs. Uncertainty draws little extra attention from spectators that eventually results in programs sales. Rather sales appear to provide information to fans at their first opportunity to view the team (first home game of the season and homecoming—often the first and only game attended by fans who travel farther). On average, 241 more programs reach patrons at the first home game each season, while an average of 90 extras sell at each homecoming. Bad weather reduces sales about 157 programs; while sweaty fans lose interest on hot days—about 4 programs for each degree Fahrenheit.

Overall, the improved results appear satisfactory for further analysis of management decisions about prices and the associated quantities they expect to sell.

Optimal Prices

Fixed Prices

The optimal program price depends on goals of the sellers and characteristics of the game listed in the independent variables. Because managers often employ a single program price for every game, which they determine before the season begins, we first compute the optimal fixed price using a typical game situation. That typical game for this study is one with the year 2000 home-team enrollment, 6459 students (headcount), current win percentage equal to the result of previous season (37.5%), real disposable income (6508.8 billion 1996 dollars), and reserved-seat price ($12 deflated to $6.95). Opponent variables (T, U, WO, and EO) assume mean values (see Table 1). Mean temperature without rain sets the stage for this game. A typical game is against a non-rival and is neither the first game of the season nor homecoming.

All variables included in the rival model figure in the optimal pricing exercise that follows, though some are effectively deleted when they take on typical values of zero, e.g., rain (R), RIVAL, and homecoming (H). The model provides the general expression Q = A + bP for the demand function. In practice, A incorporates particular (often average) effects of all the variables (except program price) and 0 or 1 for dummy variables appropriate to the situation being optimized:

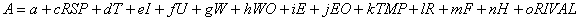
Solving for P yields 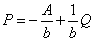, which slopes downward because b < 0. Total revenue (TR) and marginal revenue (MR) as functions of Q are: 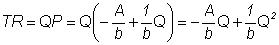and .

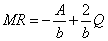The optimal Q (Q*) that will maximize revenue occurs when MR = 0. This will be Q* = A/2. Attempts to sell a quantity larger than Q* will diminish total revenue. The P function provides the price that clears the market of the Q* programs.

For the Rival-OLS model and the typical game described in the first paragraph of this section (note that RIVAL = 0), these equations are:

(5) Q = 923.24 – 353.86 P

(6) P = 2.61 – 0.0028 Q

(7) TR = 2.61 Q – 0.0028 Q²

(8) MR = 2.61 – 0.0056 Q

Consequently, for a typical game, the optimal quantity to prepare for sale is 462 programs and the optimal nominal (real) price is about $2.25 ($1.30 in 1992-1994 dollars). See the prices and quantities in Table 6 under Fixed Price. If managers seek to maximize circulation, or advertising revenue, where that is proportional to circulation, they should charge the revenue-maximizing price.

To maximize profit, MR must be the same as MC. The optimal quantity that does this must satisfy:

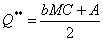
and the respective P^** derives from the above P equation (6) again. The average nominal (real) cost of a program during the 90s is about $1.95 ($1.30).[11] If all extra programs can be ordered at this cost, the AC curve will be flat and MC = AC. Assuming this to be the case for demonstration purposes, the optimal nominal (real) prices and quantity from the Rival-OLS model would be $3.37 ($1.95) and 232 programs. (See the lower half of the Fixed price column in Table 6). The optimal P is similar to the current $3 price.

Overall profits may not be maximized, if advertising revenue fluctuates with readership. Diminished readership may subvert other goals of informing and increasing interest as well. Regardless of the optimal advertising situation (a major issue apart from program sales because many advertisers buy space from loyalty and community service considerations[12]), optimal prices and quantities remain at issue for managers. The closeness of these optimal prices to the current price must please the current management. The results even suggest room for price increases.

Flexible Prices

Although it is not standard practice among college football programs, one strategy a profit-maximizing monopolist should adopt whenever possible is market segmentation by demand elasticity. One way to accomplish this segmentation would be to charge different prices for programs for “special issues,” such as for the first game of the season and homecoming.

If the administration allows flexible pricing from game to game, the model provides easy solutions. The A value in the formula would change, because dummy variables assume a value of one for the unique characteristic of the game (e.g. F = 1 for the first home game, so Q = 1164.13 – 353.86P). Table 6 displays the different possibilities.

The Rival-OLS model suggests a nominal price of $2.84 (say $2.75 or $3 for ease of making change) to maximize revenue and $3.96 to maximize profits at the home opener. If the rival is the opponent, this price further increases to $3.16 to maximize revenue and $4.28 to maximize profit.

For homecoming, $2.47 maximizes revenue, while $3.59 maximizes profits. If the rival is the homecoming opponent, the price rises to $2.79 to maximize revenue and $3.91 to maximize profit. Changing prices during the special atmosphere of homecoming might not surprise spectators, so managers could find this a suitable game for flexing their "monopoly power." Otherwise, flexible-pricers risk loss of goodwill, a particularly severe cost to college athletic programs.

If a typical game (not homecoming or the first game) is played against the rival, the revenue and profit maximizing prices are $2.57 and $3.69. All of the special game situations, mentioned so far, positively influence optimal prices.

If flexibility allows managers to set the price close to game time, they can include the weather forecast as well. Of course, rain lowers sales expectations, which requires lower prices to realize those sales as Table 6 shows.

This price flexibility will not help if the quantity available for sale is not also flexible. If the goal is to sell all available programs, the model provides a price that achieves this as well. The manager simply substitutes the quantity available for sale in the appropriate P function.

Forecasts

The home team’s overall quantity decisions occur in the spring when the manager contracts with the printer. This is the first opportunity for a forecast to benefit decision-making. The model could inform pricing decisions relying on quantity forecasts, especially in a fixed-price regime. Managers could use the sum of individual game forecasts, from the appropriate model for each game, which would sum to an overall contract quantity. However, managers can change individual game run totals as the season progresses. Later orders allow for more accurate individual-game forecasts with more up-to-date information about the game situation and specific independent variable values, such as win record and weather.

For instance, given the current nominal (real) price of $3 ($1.74) and the specific values mentioned earlier in the optimization computations, the Rival-OLS model forecasts 527 programs sold for the 2000 season opener. Programs sold out with about 335 programs. Table 7 shows forecasts for the other games that were not sellouts (recall sellout games are omitted from the sample used to estimate the model).

Analysis of the forecast errors for the year 2000 out-of-sample games yields mixed results (Table 7). The mean absolute error (MAD) of these forecasts is about 109 programs and the root-mean-square-error is about 121 programs. Not surprisingly, both values are larger than the same measures for the within-sample observations used to estimate the Rival model (Table 4). But they are both surprisingly close to the standard error of the estimate for the within-sample observations, 111 programs. The mean percentage absolute error (MAPE) is about 41%, which indicates the forecasts stray compared to the within-sample value of 27%. While these values are not what we prefer, remember they represent forecasts for games that lie outside the sample we use to estimate the model. On a more positive note, when we form 95% prediction intervals using the standard error of the estimate from the Rival model, all five predictions fall in their respective intervals. In fact, all five are within 1.5 standard errors of the actual.

These results may also reflect structural changes that accompany a new athletic management. Often new managements (and new coaches) represent the end of one regime and the start of a new one. In such cases, spectators may withhold program purchases or even stay at home, because they expect the first season in the new regime to be a poor (or rebuilding) one, and hence uninteresting. Others may be upset by personnel changes and the loss of favored coaches or individual players. Specifically, in addition to lowering ticket prices, the new management improved recruiting, and made a variety of minor changes. Lower ticket prices go against the secular trend present in the 1989-1999 data we employ, when ticket prices only increase, never fall. This also indicates that the year 2000 season is different from the preceding eleven.

Other chances for errors increase when forecasting sales for games outside the estimating sample. November 2000 was the coldest November on record, and two of the games were especially affected by extremes. In one case, the temperature was 64 at the start of the game but dropped drastically during the game while the wind surged.

Other information might improve the error evaluations. For instance, the first game sold out, so its forecast error is unobservable. Otherwise, the overall forecast error measures might decrease. In fact, use of this model would have initiated a larger printing for the first game and reduced the chance of a sellout. The error for the traditional rival (not the rival identified in the LMS stage) decreases if we adjust the forecast with the rival coefficient. Finally, data for other forecasting methods, especially prior forecasts by athletic managers, are not available for further comparison.

Conclusions

Using OLS and LMS estimation techniques, we derive and refine a model for the sales of programs at home football games. Previous research on the modeling of attendance at such games appears in the reduced form model we estimate.

The outlier-resistant estimation technique, LMS, provides significant information, which improves results for program sales. In particular, LMS distinguishes outliers, which we examine for common characteristics not included in the model. These findings suggest a modified model that accounts for the effect of playing a particular annual rival. Surprisingly, the prevalent preconception that excess demand occurs at games with the traditional rival proves unfounded. The estimated model already incorporates any such special effect.

Mindful of other program sales objectives, such as enhancement of the institution’s image, prestige, and community presence, athletic directors can use the improved model to assist their efforts to set prices in order to maximize revenues and/or profits. Optimal fixed program prices exceed the actual price over almost all of the sample years. However, revenue-maximizing prices fell below the 2000 season price, while profit-maximizing prices exceeded it. Allowing flexible prices from game to game, managers should charge higher prices for programs on special event days, such as the first game of the season, homecoming game, and games against special rivals. This paper illustrates a technique that quantifies and controls for these factors, then takes advantage of them to illustrate the attainment of typical management goals.

References

Cairns, J.A. (1987). Evaluating changes in league structure: the reorganization of the Scottish Football League. The Economic Record, 63, 220-230.

Cairns, J.A. (1990). The demand for professional sports teams. British Review of Economic Issues, 12(28), 1-20.

Cairns, J.A.; Jennett, N.; & Sloane, P.J. (1986). The economics of professional team sports: a survey of theory and evidence. Journal of Economic Studies, 13(1), 3-80.

Cebula, R. J.; Austin, R.; Wildener, K.; & Belton, W. J. (1997). The impact of public mass transit on the operating income of professional sports franchises in the United States: A preliminary analysis for the NFL, MLB, and NBA. Journal of Sport Management, 11, 335-342.

Peel, D. & Thomas, D. (1988). Outcome uncertainty and the demand for football. Scottish Journal of Political Economy, 35(3), 242-249.

Ramsey, J. B. (1969). Tests for specification errors in classical linear least quares Regression Analysis. Journal of the Royal Statistical Society, Series B, 31, 350–371.

Ramsey, J. B. and Alexander, A. (1984). The econometric approach to business-cycle analysis reconsidered. Journal of Macroeconomics, 6, 347–356.

Rottenberg, S. (1956). The baseball-player’s labor-market. Journal of Political Economy, 64(3), 242-258.

Rousseeuw, P. J. (1984). Least median of squares regression. Journal of the American Statistical Association, 79(388), 871-880.

Rousseeuw, P. J. (1997). Robust regression, positive breakdown. Encyclopedia of Statistical Sciences, Volume 1, Update, eds. S. Kotz, C.B. Read, and D.L. Banks, (John Wiley & Sons, New York).

Rousseeuw, P. J. & Leroy, A.M. (1987). Robust regression and outlier detection. New York: John Wiley & Sons.

Schofield, J.A. (1983). Performance and attendance at professional team sports. Journal of Sports Behaviour, 6, 196-206.

Siegfried, J.T. & Eisenberg, J.D. (1980). The demand for minor league baseball, Atlantic Economic Journal, 8(2), 59-69.

Siegfried, J.T. & Hinshaw, C.E. (1979). The effect of lifting TV blackouts on professional football no-shows, Journal of Economics and Business, 32(1), 1-13.

Welki, A.M. & Zlatoper, T.J. (1994). US professional football: the demand for game day attendance in 1991. Management and Decision Economics, 489-495.

White, H. (1980). A heteroskedasticity-consistent covariance matrix and a direct test for heteroskedasticity. Econometrica, 48, 817–838.

TABLE 1

VARIABLE INFORMATION

Symbol	Variable	Measure	Mean	St. Dev.
Q	Program Sales per game	Number of programs	359.77	156.95
P	Program Price	Real 1982-1984 dollars	1.47	0.2
RSP	Reserved Seat Price	Real 1982-1984 dollars	8.14	0.67
T	Travel Costs	Hours between opponent's & home-team's sites	4.35	1.74
I	Income	Average Real Disposable Income1982-1984 dollars	5545.86	489.47
U	Uncertainty	Ratio of Win Percentages*	0.52	0.31
W	Home Win Percentage	Percentage of Games won**	40	22
WO	Opponent Win Percentage	Percentage of Games won**	55	31
E	Home Enrollment	Fall Headcount	6622	209
EO	Opponent Enrollment	Fall Headcount	6191	4544
TMP	Temperature during game	Degrees F	65.9	9.49
R	Rain	1 signifies rain during game; 0 for no rain	0.14	0.35
F	First Home Game of Season	1 signifies first home game of season; 0 otherwise	0.2	0.4
H	Homecoming	1 signifies a homecoming game; 0 otherwise	0.2	0.4
RIVAL	Opponent with special impact	1 signifies special rival (not traditional rival)	0.04	0.19

Notes: * Lowest win percentage/highest win percentage

** Cumulative for season or last season record if season opener is at home

Table 2

Correllation Matrix

	Q	P	F	H	A	RSP	T	I	U	W	WO	E	EO	Tmp	R	Rival
Q	1.0000
P	0.0075	1.0000
F	0.3530	0.0017	1.0000
H	0.1201	-0.0096	-0.2444	1.0000
A	0.7367	-0.0079	0.0549	0.2647	1.0000
RSP	-0.2745	-0.3868	-0.0115	-0.0301	-0.1096	1.0000
T	-0.1777	-0.1095	-0.1393	0.1027	-0.3103	-0.0232	1.0000
I	-0.2507	0.3758	-0.0588	-0.0262	-0.0955	0.0523	0.0106	1.0000
U	-0.0608	-0.1876	-0.1294	0.0822	0.0921	0.2694	-0.1382	-0.0174	1.0000
W	0.0273	-0.2490	-0.1321	-0.0386	0.1921	0.2577	-0.2853	-0.1296	0.3988	1.0000
WO	0.3292	-0.0098	0.0413	-0.0966	0.3465	-0.2114	0.0013	-0.1199	-0.0224	-0.0240	1.0000
E	-0.1948	-0.7645	0.0006	0.0006	-0.0223	0.3706	0.1706	0.0398	0.3199	0.3024	0.0003	1.0000
EO	0.0138	0.0138	-0.2926	-0.2003	0.1292	-0.0886	0.0203	-0.0758	0.1951	0.1631	0.2016	0.0812	1.0000
Tmp	0.1206	0.1128	0.4253	0.0095	-0.0340	-0.0282	-0.0887	0.0696	-0.2779	-0.1984	0.1505	-0.1448	-0.1733	1.0000
R	-0.3203	-0.2248	0.1835	-0.2018	-0.3491	0.3282	-0.1501	-0.1204	0.2297	0.1731	-0.0540	0.2235	-0.2311	-0.1698	1.0000
Rival	0.2119	-0.0288	0.3892	-0.0951	0.1247	-0.1766	-0.2161	-0.1700	0.0930	0.0130	0.1250	0.0523	-0.1243	-0.0391	0.1964	1.0000

Table 3
STRUCTURAL ESTIMATES OF PROGRAM DEMAND EQUATIONS
	OLS		TSLS		Block Recursive
Variable	Coef	Two-tail P-Value	Coef	Two-tail P-Value	Coef		Two-tail P-Value
P	10.1471	0.1518	10.4298	0.8992	19.4225		0.8155
A or A-hat¹	0.04490	0.0000	0.04908	0.0000	0.05007		0.0000
F	123.46	0.0007	120.1294	0.0063	181.722		0.0000
H	2.8800	0.9354	-4.8617	0.9143	73.5060		0.0862
constant	-97.4487	0.3831	-134.594	0.3657	-184.512		0.2417

Standard Error	97.6		119.6		120.9
R-SQUARE	64.1		46.1		44.9
F	227604	0.0000	10.905	0.0000	10.416	0.0000
DOF	51		51		51
N	56		56		56
¹ Actual attendance (A) is used in the OLS regression. Fitted values (A-hat) are used in the TSLS and block recursive regressions. TSLS instruments are RSP, T, I, U, W, WO, E, EO, Tmp, R, P, F, and H. In the block recursive estimate, A-hat is the fitted value from a regression of RSP, T, I, U, W, WO, E, EO, Tmp, and R on A.

Table 4
REDUCED-FORM PROGRAM DEMAND ESTIMATES
	OLS		RWLS		RIVAL-OLS
Variable	Coef	Two-tail P-Value	Coef	Two-tail P-Value	Coef		Two-tail P-Value
P	-321.8655	0.0735	-450.907	0.0000	-353.8582		0.0404
RSP	-25.61065	0.3851	-30.07882	0.0697	-26.45297		0.3460
T	-11.18703	0.2862	20.99088	0.0012	1.39254		0.9019
I	-0.00205	0.9649	-0.00581	0.8056	0.01250		0.7801
U	23.07945	0.7110	36.11487	0.2219	4.23241		0.9435
W	1.06479	0.2364	1.88172	0.0002	1.30929		0.1310
WO	1.58098	0.0064	0.07125	0.8189	1.25182		0.0263
E	-0.33615	0.0425	-0.57693	0.0000	-0.39180		0.0151
EO	0.00124	0.7760	0.01063	0.0002	0.00515		0.2541
TMP	-3.82874	0.0672	-6.77738	0.0000	-3.97454		0.0468
R	-180.8259	0.0021	-157.7383	0.0000	-156.7327		0.0055
F	229.88	0.0000	409.4503	0.0000	240.8869		0.0000
H	89.45138	0.0556	90.4235	0.0010	90.01424		0.0435
Rival					130.9947		0.0247
constant	3391.803	0.00549	5181.333	0.0000	3659.983		0.0020

Standard Error	116.6		87.1 ¹		110.9
R-SQUARE	57.8		91.6		62.8
F	4.433	0.0001	23.572	0	4.938	0
DOF	42		28		41
N	56		42		56

# OF OUTLIERS
Included Data	0²		0		1²
Excluded Data			14

White Test	26.08	0.3	22.63	0.48	31.82	0.13
Ramsey RESET F
Second Order	0.075	0.78	0.004	0.95	0.119	0.73
Third Order	0.707	0.49	0.065	0.94	1.560	0.22
Fourth Order	2.113	0.11	1.866	0.16	1.320	0.28
Fifth Order	1.565	0.20	1.476	0.24	1.404	0.25

¹ This is a scale estimate produced by LMS and similar to the typical standard error of the estimate.
² These are standardized residuals. For other outlier techniques see Table 5.

Table 5

Identified Outliers by Technique

Table 7
Sales Forecast Results

Forecast	Forecast Interval	Actual	Error	Standardized Error
344	(126.6, 561.4)	240	104	0.9
376	(158.6, 593.4)	345	31	0.3
391	(173.6, 608.4)	307	84	0.8
329	(111.6, 546.4)	499	-170	-1.5
334	(116.6, 551.4)	176	158	1.4

	Error Analysis
		Within Sample	Outside Sample
	MAD	76.3	109.4
	MAPE	27.2	40.7
	MSE	9006.7	14539.4
	RMSE	94.9	120.6
	Standard Error	110.9

Endnotes

We would like to thank various people for their assistance: Brenda Moore in the Interlibrary Loan section of Hunter Library at Western Carolina University; William Crocker, Derik Briggs, and Muniza Haq, graduate assistants in the MBA program; Kevin Ayers, Director of the WCU Sport Management Program; Jeff Compher, Athletic Director; Jody Jones, Sports Information Director; and especially two people: Hunter Yurachek, Senior Associate Athletic Director and Steve White, retired Sports Information Director and current encyclopedia of sport lore and detailed facts at WCU. All assisted us generously and without them we could never have produced this paper. Normally, authors accept responsibility for all errors, but we have much greater confidence in our work thanks to Hunter and Steve. We also wish to thank Nick Rupp, Gerald Granderson, and three anonymous referees of the Journal of Sport Management for much helpful comment and advice. Their involvement greatly improved the quality of the paper.