Baseball Card Pricing Model:
A Demonstration with Well-Known Players
VISIONS IN
LEISURE AND FITNESS (2004)
By
Robert F.
Mulligan, Assistant Professor
Department of
Business Computer Information Systems and Economics
A.J. Grube,
Assistant Professor
Department of
Health and Human Performance
Stephen B.
Jarrell, Professor
Department of
Management and International Business
INTRODUCTION
The economic literature
on appreciation of non-financial investment assets has generally found low
rates of return accompanied by high risk.
Assets studied have included real estate, artworks, wines, and sports
memorabilia. Sports memorabilia comprise
an especially promising subject for further study. One essential feature rendering sports
memorabilia more favorable subjects is the relative homogeneity of collectibles
such as baseball cards, a feature clearly not shared by artwork or real
estate.
All cards of a
certain issue should have their value determined by characteristics intrinsic
to the card, such as a card's age, condition, and scarcity, and characteristics
extrinsic to the card, such as the particular player's records, fame, and
popularity. Intrinsic characteristics
are generally properties of the whole issue and are shared by all cards of a
given year printed by a given manufacturer, assuming that equal numbers of each
player were printed. Obscure player's
cards will be sought to complete sets of a given issue, and famous or star
player's cards will face additional demand to complete sets or enhance partial
sets of star player or team cards.
This paper
develops a simple hedonic pricing model for baseball cards, of the type often
used successfully to model prices for artworks.
We estimate this model with an illustrative sample of card prices for
several different years. The results are
used to demonstrate the construction of price indices (i.e. rates-of-return)
for baseball cards for this particular set of cards using two methods. Finally, we extract specific values that
individual player characteristics contribute to the value of a card. The paper is organized as follows: a review
of the literature is followed by a development of the hedonic pricing model and
consequent price indices, a discussion of the data used, presentation of the
empirical results, and finally the conclusion.
LITERATURE
This section
discusses some of the relevant economic literature on pricing sports
memorabilia and other non-financial investment assets, such as artwork. Stoller [1, 1984] provides a valuable
analysis of the Fleer v. Topps antitrust case as well as a discussion of the
underlying economics of the baseball card business. The loss of Topps' monopoly power in 1980 and
the introduction of competition [1, 1984, p. 23] may have caused the collapse
of a speculative bubble in card prices.
Stoller [1, 1984, p. 19] documents a 31.6 percent annual return on Topps
cards.
Nardinelli and
Simon [7, 1990] and Andersen and La Croix [1991] both found that a player's
race significantly affected the price paid for baseball cards on the secondary
market. These studies focus on the
secondary market for sports memorabilia to isolate consumer discrimination from
co-worker and employer discrimination.
McGarrity, Palmer, and Poitras [6, 1999] found little evidence of racial
discrimination in the market for baseball cards. They used a dataset with constant supply,
where effects from speculative demand are largely removed by considering only
retired players. Using a variety of
econometric specifications allowed them to assess the robustness of their
results. Fort and Gill [5, 2000] study
racial discrimination in baseball card markets using continuous, non-binary
racial perceptions of market participants, as reported by surveys. They find evidence of discrimination against
black and Hispanic hitters and against black pitchers, but not Hispanic
pitchers. The mixed results leave no
clear indication of the impact of racial discrimination on baseball card
prices.
The literature
on pricing artwork has significant implications for sports memorabilia
markets. Ekelund, Ressler, and Watson
[4, 2000] examine how an artist's death affects the demand for that artist's
work. They find a clustered rise in the
artwork's values immediately around the time of the artist's death. This phenomenon has two implications for the
sports memorabilia market. The supply of
baseball cards is effectively frozen for a particular player when the player
retires from the game, rather than at death.
Ancillary memorabilia, including autographs, and public appearances can
continue to generate nostalgia and interest in a player, enhanced by the
player's death.
Rengers
and Velthuis [8, 2002] and Agnello and Pierce [1,
1999] study determinants of artwork prices based on characteristics of the
artwork, artist, and gallery. This approach generalizes fairly readily to
baseball cards, which have characteristics attributable to the player, team,
and year of issue. Reneboog and Van
Houtte [9, 2002] and Agnello and Pierce [1, 1999]
find that artworks significantly underperform when compared with financial
assets, owing to the very high risk of investing in art, the heterogeneity of
artworks, high transactions costs, and high costs of insurance, transportation,
security, and resale. It is particularly
worth noting that none of these negative features generally applies to sports
memorabilia. Baseball cards of a given
player, issue, and condition are always non-unique, homogeneous assets.
Clearly,
researchers have laid much of the groundwork for estimating financial models
for investment in baseball cards. We
build on this foundation of art models with research on similar relevant
factors for a limited set of baseball cards.
MODEL
Baseball cards
appreciate in value in a fashion similar to wine, though for different
reasons. The supply of cards of a
particular brand, player, and year is limited to the number printed. Surviving copies appreciate in value, as some
are lost, destroyed, or decay in condition as time passes. This gradual diminution of the supply of
cards is similar to what happens as vintage wines are consumed, mature forests
are harvested for lumber, or petroleum deposits are pumped out of the
ground. Unlike wines, baseball cards and
other sports memorabilia do not acquire chemical changes as they age which
improve their quality, and desirability.
In fact, the chemical changes to which sports memorabilia are subject
over time normally detract from their desirability, and collectors attempt to
prevent or delay chemical changes.
Changes in
demand also affect the prices of sports memorabilia. Demand for such memorabilia increases with
interest in the particular sport or athlete, with interest in the memorabilia
for its own sake, and with increased chances of return on them as investment
assets. Demand effects can occasionally
be negative, as documented for the collapse of baseball card prices caused by
the end of monopoly pricing in 1980 [10, 1984, p. 23], an exceptional event in
this market.
Sports
memorabilia and athletes have unique characteristics as well. Though old baseball cards of comparable
significance, condition, and quality are generally more valuable than newer
cards, the career performance and general fame of the player make a card more
desirable and therefore more valuable.
All cards of a given issue had the same price when new, and appreciate
over time. A rookie card of an average
player appreciates much less than that of a better-known player. A rookie card of a presumed hot-prospect may
appreciate rapidly early on, but plateau or even decline in value as the
player's career fails to achieve its initial promise. Some players' cards are especially desirable
due to tragically brief careers. To
capture the effect of factors that distinguish among a group of well-known
players, we augment the model with variables, such as hall-of-fame induction,
and death.
A hedonic price
model incorporates these effects in a manner that is useful for evaluating the
value and prospects for cards as an investment.
The generalized form of the model is:
ln
Pt = ∑atXt + ∑btZt
+ et
Where
X and Z are vectors of observable characteristics, extrinsic and intrinsic,
respectively, to a specific card. The natural logarithm of price, ln Pt, is typically employed
in these models and avoids the problem with extremely large or small prices.
Extrinsic
characteristics are associated with specific players and vary across cards of a
specific year. Estimates of the effects
of such variables are useful to investors, because they show the typical change
in price whenever one of these explanatory factors changes. For example, if a player improves his batting
average, appears in the World Series, or is elected to the Hall of Fame, then
we expect his card value to increase.
Economists call these values shadow
prices, because they show the price of the factors or how investors value
the factors.
When we include
such extrinsic factors in the model, we are able to separate and distinguish
the combined play of intrinsic factors, such as deteriorating cards,
diminishing supply, and breaking of records.
These factors affect all cards issued during a single season, and we
assume they affect all cards similarly, that is, at the average effect. To avoid multicollinearity,
a single trend variable or a related series of time dummy variables capture the
effect of these intrinsic factors simultaneously.
Using a(t) momentarily to represent the intrinsic pattern (and
dropping the error term for simplicity), the model is:
ln P = a + b Black + c HallFame + d BatAvg + e
WrldSer + f Rookie + g Deceased + a(t)
Building on the
significant literature concerning race, we include a dummy variable for race in
the specification. Election
to the Hall of Fame and batting average measure a player's actual performance. Note that earned run average would be used
for pitchers, who would generally have to be priced with a separate model. The number of World Series appearances
improves the desirability of a player's cards (a player's team is more likely
to make it to the World Series the better the player's performance). Many collectors desire rookie cards, which
are generally more rare, especially for famous
players. If rookie cards are valued in
any way differently from ordinary cards, including a dummy variable for rookie
card status should improve the model's forecasting performance. Table 1 includes a complete list of variable
definitions.
{{INSERT TABLE 1 ABOUT HERE}}
In this model
format, a coefficient, such as d represents the approximate proportionate
change in card price when the factor (batting average) increases by one point
(we express batting averages as whole numbers for easier interpretation of
results). For a qualitative variable,
such as Black or Rookie, it is the approximate proportionate change in card
price when the player or card fits a certain category. We usually transform the coefficient to 100(ed
–1) to obtain a better approximation
of the effect in percentage terms. The
base for the percentage change is the rpice of a
particular card where all variables except the one being interpreted are held
constant. For instance, 100(ed-1) is the approximate
percentage change in Rookie card price for a one-point increase in the batting
average of a Black Hall-of-Famer with 2 trips to the World Series as of
1983.
Several
intrinsic factors relate to a player’s age.
Generally cards of older players should be more valuable. The number of years elapsed from the start of
a player’s career and from the end of that career,
career longevity itself, age of a player, and age of the card are closely
related. They all change with the
passage of time. To avoid
multicollinearity problems, we allow a(t) to capture
their combined effects.
The time
function, a(t), appears in two formats. The simpler case adds a single term with a
trend variable, t, to the model. In this
case, a(t) becomes ht,
where h is the coefficient of t. eh quantifies the relative price of a card from
one year to the next. The assumption in
this case is that the annual percentage change is constant over the 20-year
period. The transformation (eh)t, for various values of t, forms a series
of indices that represent price changes, and 100(eh-1) produces the approximate annual percentage
change or rate of return.
The second a(t) case uses seven dummy variables for the different
periods (1982 is the omitted period, so it is the base year for indices and
return rate calculations), so
a(t) = h83D83 + h84D84
+ h85D85 + h88D88 + h93D93
+ h99D99 + h02D02
To determine the
price advance from the base year (1982), we use the coefficient of the year i dummy variable (hi) to obtain
. This allows for
different rates of price changes during different time periods, a less
restrictive model. This form allows for
unexpected fluctuations and specific events, such as the 1980 price
collapse. We discuss estimates of both
models in the results section, where we use the above transformations to
interpret the results.
DATA
This section
documents the data we use to estimate the model. A convenience sample of twelve well-known
players, listed in Table 2, illustrates the estimates, analysis, and
interpretation of the model. The sample
is not random and is biased toward familiar talented players, which limits the
generalizations we can make. Instead, we
present the model as a demonstration of the method and a basis for further
research.
{{INSERT TABLE 2 ABOUT HERE}}
Internet
sources, from baseball-reference.com, provided extensive data on extrinsic
variables for individual players. Prices
for one card for each player were taken from the Price Guides for eight
different years over a twenty-year span from 1982 to 2002. One significant difference between these data
and the auction prices used in empirical examinations of artwork prices should
be noted. Artworks are unique and each
auction price for a given artwork records a unique transaction at a unique
point in time. In contrast, the Price
Guide observations of card price in a given year are taken from dealer
surveys. There is never any specific,
single exchange that can be documented at the listed price. Generally, the Price Guide is used as an
authority for dealers to price and update their inventory. Many transactions occur at the price listed
in the Price Guide because it is widely accepted as an authoritative
source. A further difference derives
from the fact that there are many identical copies of a given card, even in the
same condition, while an artwork is always absolutely unique.
RESULTS
This section
presents the estimated results. Table 3
displays the actual estimates of the models; single trend term under “constant
change” and the assortment of time dummy variables under “flexible change”. Overall, the results are good. High R-squares and F-values suggest both
models offer investors and collectors a useful tool.
{{INSERT TABLE 3 ABOUT HERE}}
Extrinsic Factors
The estimates of
coefficients of the extrinsic factors, the ones that distinguish individual
players, are generally good. The results
are very similar for both models of time (intrinsic) changes. Overall, that the model produces any
significant findings amongst the twelve renowned players attests to the
importance or robustness of the variables.
Consider player
performance variables, BatAvg, WrldSer,
and HallFame, measures of player performance. They produce different results. Higher batting averages do produce
statistically significant higher prices, as expected. Using the transformations suggested earlier,
the estimated impact of a one-point increase in the batting average is a
2.63-2.68% increase in the card price. However, the coefficient of Hall of Fame
is negative and insignificant in both models.
Indirect player performance, reflected by number of World Series
appearances, is also significantly positive.
An additional appearance is calculated to bring an average price
increase of 40-41%. Batting average and
number of World Series appearances may account for the unexpected Hall of Fame
estimate. It is probably too much to ask
for all variables for outstanding-performance for these sampled players to show
a strong impact on price.
Results with the
qualitative variables are mixed as well.
Race coefficients are positive and significant for Black players. The magnitude is surprising, ranging from
140% to 151%. There is no evidence that
rookie cards and death of the player enhance the value of cards among these
players. Perhaps these variables work
differently for a gifted set of players.
Intrinsic Factors:
Price Indices and Rates of
Return
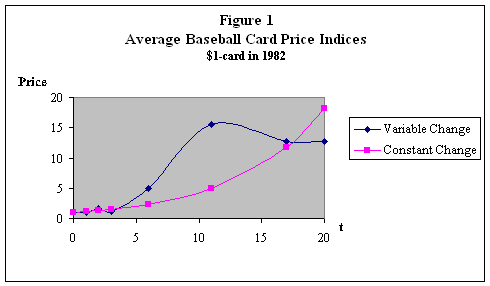
Figure 1 and
Table 4 contrast the findings for the price indices from the two models for the
intrinsic variables. The flexibility of
the variable-change or dummy variable approach is obvious.
{{INSERT FIGURE 1 AND TABLE 4 ABOUT
HERE}}
The model with
the single time variable, t, produces a significantly
positive coefficient. When transformed,
the coefficient indicates that prices of cards in this group increase by about
15.63% per year. This is an estimate of
the annual rate of return. Figure 1
depicts such an increase over the 21-year period for a card that was priced at
$1 in 1982. The dollar value on the vertical
axis is also the price index (expressed as a proportion rather than a percentage)
for that period.
In contrast, the
dummy variable approach produces seven coefficients (five are significant)
coefficients and a variable-path of prices and return rates. We can solve for an approximate constant
annual growth rate that would produce the change from 1982 to period i by using 
. For instance, the
index of 1278 in 2002 means that a card that cost a dollar in 1982 and
increased in value by 13.59% per year, would be worth
$12.78 in the year 2002. The shaky early
start in the 1980s probably reflects the 1980 monopoly-price disruption. Subsequently, the market took off, and then
seemed to level off in the late 1990s, when record stock performances may have
attracted investment funds away from cards.
The slowed economy in 2002 could account for the reduced return in this
year. The flexible change approach
allows for such a path, while the constant change forces the change to grow
ever larger and in the same direction.
Either approach
shows that cards for this sample were earning a very good return with some
calculations showing values that approach the 31.6% of Stoller. The choice of time span can affect these
estimates. A high rate of return is not
surprising given the selection of players.
The hedonic price model and both time approaches provide some image of
the behavior of baseball cards over the period.
A more comprehensive data set, perhaps with dummy variables to identify
particular players, offers the potential for better guidance for investors.
CONCLUSION
A hedonic
pricing model was estimated on a sample of twelve baseball cards with prices
observed in eight different years over a twenty-year period to demonstrate the
approach for sports memorabilia. This
model was estimated separately for two different approaches or assumptions
about rates of return. Both models
performed extremely well and explained differences among baseball card prices
for the limited group of cards in the sample.
Future research should include a more comprehensive data set.
Among extrinsic
variables that represent specific player and card characteristics that
differentiate cards issued during the same season, race had a significant
positive effect on price for Black players.
Batting average and number of World Series appearances had significant
positive impacts on price, but surprisingly, rookie cards tended to be worth
relatively less than non-rookie cards.
In addition, a player's death and election to the Hall of Fame generally
decreased the value of his cards. The
unexpected findings may result from trying to estimate too many enhancements
among a group of extraordinary players.
Price indices
and rates of return estimates resulted from the two approaches to measuring
intrinsic effects, effects that occur to all cards issued during the same
season. Among the sampled cards, the
return estimates indicated a set of good investments on average.
REFERENCES
1. R.
Agnello and R. Pierce, Investment Returns and Risk for Art: Evidence from
Auctions of American Paintings (1971-1996), Working
Paper,
2. T.
Andersen and S.J. La Croix, Customer Racial Discrimination in Major League
Baseball, Economic Inquiry, Vol. 29, pp. 665-677, 1991.
3. Baseball-reference.com,
http://www.baseball-reference.com/, November 2002.
4. R.B. Ekelund, R.W. Ressler, and J.K.
Watson, The "Death Effect" in Art Prices: a
Demand-Side
Exploration, Journal of Cultural
Economics, Vol. 24, pp. 283-300, 2000.
5. R. Fort and A. Gill, Race and Ethnicity
Assessment in Baseball Card Markets, Journal
of
Sports Economics, Vol. 1(1), pp. 21-38, 2000.
6. J. McGarrity, H.D. Palmer, and M.
Poitras, Consumer Racial Discrimination: a
Reassessment
of the Market for Baseball Cards, Journal
of Labor Research, Vol. 20(2),
pp. 247-258, 1999.
7. C. Nardinelli and C. Simon, Customer
Racial Discrimination in the Market for
Memorabilia:
the Case of Baseball, Quarterly Journal
of Economics, Vol. 105, pp. 575-
595, 1990.
8. M. Rengers and O. Velthuis,
Determinants of Prices for Contemporary Art in Dutch
Galleries, 1992-1998, Journal of Cultural Economics, Vol. 26,
pp. 1-28, 2002.
9. L. Renneboog and T. Van Houtte, The Monetary Appreciation of Paintings: From
Realism to Magritte,
10. M.A. Stoller, On the Economics of
Antitrust and Competition in a Collectibles Market:
the Strange Case of the Baseball Card Industry, Business Economics, Spring 1984, pp.
18-26.
|
Table
1 Variables
in the Hedonic Price Model |
|
|
P |
= card price in current dollars from the Price
Guides |
|
BLK |
= 1 if player is Black, = 0 otherwise |
|
HallFame |
= 1 if player was in Hall of Fame prior to
year of Price Guide, = 0 otherwise |
|
BatAvg |
= player career batting average up to and
including year of price observation, t |
|
WrldSer |
= number of world series appearances prior to
year of Price Guide |
|
Rookie |
= 1 if card is a rookie card, = 0 otherwise |
|
Deceased |
= 1 if player was deceased prior to year of
Price Guide, = 0 otherwise |
|
t |
= year of observation, 1982 = 0 |
|
Dt |
= 1 if price observed in year t, = 0 otherwise |
|
Price Guides from 1982, 1983, 1984, 1985,
1988, 1993, 1999, and 2002. |
|
|
Table 2 Sample of Baseball Cards |
||||
|
Player |
Years Played |
Teams |
Card Issuer and Year |
Card # |
|
Aaron, Hank |
1954-76 |
MLN ATL MIL |
1954 Topps |
128 |
|
Bench, Johnny |
1967-83 |
CIN |
1968 Topps |
247 |
|
Brett, George |
1973-93 |
KCR |
1975 Topps |
228 |
|
Carew, Rod |
1967-85 |
MIN |
1967 Topps |
569 |
|
Fisk, |
1969-93 |
BOS CHW |
1972 Topps |
79 |
|
Jackson, Reggie |
1967-87 |
KCR OAK BAL NYY |
1969 Topps |
260 |
|
Mantle, Mickey |
1951-68 |
NYY |
1952 Topps |
311 |
|
Musial, Stan |
1941-63 |
STL |
1948 Bowman |
36 |
|
Robinson, Jackie |
1947-56 |
BRO |
1949 Bowman |
50 |
|
Rose, Pete |
1963-86 |
CIN PHI MON |
1963 Topps |
537 |
|
Williams, Ted |
1939-42 & 1946-60 |
BOS |
1950 Bowman |
98 |
|
Yastrzemski, Carl |
1961-83 |
BOS |
1960 Topps |
148 |
|
Table 3 Models of Baseball Card Prices |
||||
|
|
Constant Change |
Flexible Change |
||
|
|
Coefficient |
Two-tail P-value |
Coefficient |
Two-tail P-value |
|
Constant |
-4.638 |
0.005 |
-4.668 |
0.001 |
|
Black |
0.9195 |
0.001 |
0.8735 |
0.000 |
|
HallFame |
-0.0904 |
0.732 |
-0.1031 |
0.648 |
|
BatAvg |
0.0264 |
0.000 |
0.0260 |
0.000 |
|
WrldSer |
0.3432 |
0.000 |
0.3366 |
0.000 |
|
Rookie |
-0.8876 |
0.007 |
-0.8961 |
0.002 |
|
Deceased |
-1.0434 |
0.003 |
-0.8642 |
0.004 |
|
t |
0.1452 |
0.000 |
|
|
|
D83 |
|
|
0.0193 |
0.948 |
|
D84 |
|
|
0.5414 |
0.072 |
|
D85 |
|
|
0.2100 |
0.482 |
|
D88 |
|
|
1.5935 |
0.000 |
|
D93 |
|
|
2.7475 |
0.000 |
|
D99 |
|
|
2.5373 |
0.000 |
|
D83 |
|
|
2.5480 |
0.000 |
|
R2 |
78.4% |
85.6% |
||
|
F (p-value) |
45.58 (0.000) |
37.48 (0.000) |
||
|
n |
96 |
96 |
||
|
Table
4 Price
Indices & Rates of Return |
|||||
|
|
|
Constant
Change |
Flexible
Change |
||
|
|
|
Price |
Annual
Rate |
Price |
Annual
Rate |
|
Year |
t |
Indices
(%) |
Since
1982 (%) |
Indices
(%) |
Since
1982 (%) |
|
1982 |
0 |
100 |
|
100 |
|
|
1983 |
1 |
116 |
16 |
102 |
1.95 |
|
1984 |
2 |
134 |
16 |
172 |
31.09 |
|
1985 |
3 |
155 |
16 |
123 |
7.25 |
|
1988 |
6 |
239 |
16 |
492 |
30.42 |
|
1993 |
11 |
494 |
16 |
1560 |
28.37 |
|
1999 |
17 |
1181 |
16 |
1265 |
16.10 |
|
2002 |
20 |
1826 |
16 |
1278 |
13.59 |
