|
|
Short Sea
Shipping: Alleviating the Environmental Impact of Economic Growth |
|
Robert F. Mulligan, Ph.D.
Western Carolina University
Gary A. Lombardo, Ph.D.
United States Merchant Marine Academy
Abstract
This paper quantifies the potential
environmental benefit of short sea shipping.
Critical strategic issues relevant to formulating public policy are
developed. Coastal
shipping has traditionally been a major sector of the maritime industry.
This continues to be the case in the European Union, but the sector has
diminished in relative importance in North America as the transport industry has
become increasingly dominated by less environmentally-friendly interstate trucking
and railroads. Congestion threatens to overwhelm overland carriage and
limit economic growth. An alternative strategy
is to revitalize coastal shipping as short sea shipping to alleviate traffic
congestion and enhance economic development by maintaining freight flow
efficiency. Because ship transport
offers higher fuel economy and lower emission of harmful pollutants, the
environmental benefits of short sea shipping over land transportation can be
quantified and used to inform public policy.
Key words: short sea
shipping, fuel economy, ship operation cost estimate, hydrocarbon emissions,
fuel consumption
1.
Introduction
This research
establishes that substituting Short Sea Shipping (SSS) traffic for overland
freight carriage in North America will result in significant alleviation of
environmental impact in addition to offering a reduction in increasingly
overburdened highway vehicular traffic. SSS
offers a possible solution in the form of an alternative transport mode as
overland carriers have become overwhelmed and undependable due to traffic
congestion. The more successful SSS
proves in achieving market share, the greater will be its impact in relieving
clogged land arteries and lowering costs of transport over competing modes, as
well as improving time performance. More
importantly, every mile a ton of freight is carried by SSS instead of by
interstate truck lines or railroads will result in reduced fuel consumption and
environmental impact.
SSS is
used extensively to transport cargo throughout the European Union. Although the United States once relied on
coastal shipping lines, traditional coastal shipping has largely been
supplanted by various kinds of overland transport, which consume more fuel and
emit more pollutants that shipping.
Overland freight carriers now face the threat of paralysis due to
economic expansion and population growth. The short sea shipping concept is reviewed; the
calculations for quantifying environmental impact are presented; public policy implications are discussed; and
a conclusion is presented. Details of
the hypothetical ship estimate are given in the appendix.
2. Short Sea Shipping
The movement of cargo by sea is an important component of the European
Union’s transportation system. The
intra-European Union sea movement of cargo represents 42% of the bulk goods
being transported[1]. Short sea shipping in Europe is viewed as
essential to alleviate highway congestion and reduce environmental pollution[2].
The characteristics
found in the transportation network for the U.S. domestic market are similar to
domestic markets found in nations with advanced economies. Most developed nations rely on a national
highway system to carry cargo, even though this is among the most expensive and
environmentally-polluting, resource-consuming, transport modes. Due to
the fact that increases in annual freight movements in the U.S. far surpass
that of annual highway mileage construction, highway congestion has become a
significant problem, as is apparent in terms of increased travel time.
Highway travel time also increases the social welfare cost due to resultant
inefficiencies. Freight movement inefficiencies are projected to increase
dramatically as US highways “. . . experienced a doubling of vehicle miles
traveled in the past twenty years while the total highway mileage has only
increased by 1%.” This general trend is expected to
continue. Projections for the next
fifteen years indicate explosive growth in cargo transport measured in both
freight tonnage and value[3].
Because SSS has to be
implemented basically from scratch for North American markets, policy makers
and the transportation industry face the challenge of developing an efficient
and effective complement to the existing transportation system they inherit. At the same time, the situation presents
opportunities because the industry is not constrained by existing
environmentally unfriendly practices or traditions, and can select from among
the most environmentally friendly capital infrastructure. The conceptual model (Figure 1) is offered to
focus discussion and eventually enhance understanding concerning the short sea
shipping concept as a commercially viable enterprise.
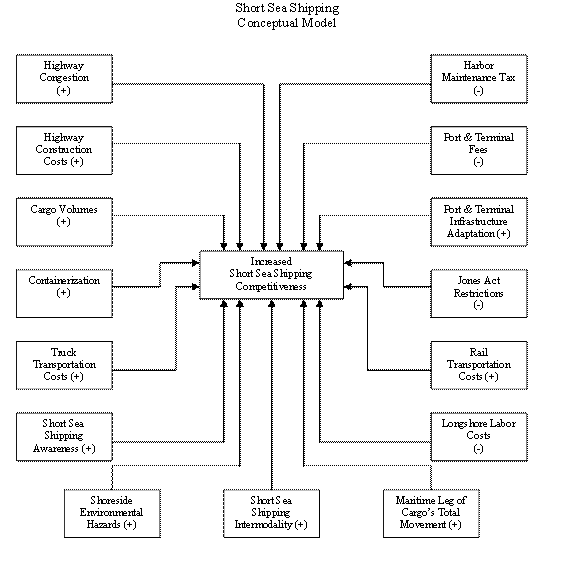
Figure 1. Short Sea Shipping Facilitating
(+) and Inhibiting (-) Factors
(Source: Lombardo 2004[4])
The extent of
congestion on the East-coast I-95 highway corridor and elsewhere needs to be
quantified by intermodal segment and a
reasonable process for estimating the additional monetary costs needs to be developed. The quantification of the congestion/travel
delay experience is a precondition for promoting awareness of short sea
shipping as a potential solution, as well as allowing for meaningful
cost-benefit analysis. Thus one data
requirement is point-to-point cargo volume and delay time for the interstate
highway system and for railroads. The economic
feasibility of short sea shipping focuses on whether it can offer lower freight
charges than overland carriage.
Whether short sea
shipping can avoid or mitigate delay times, either by bypassing or alleviating
overland congestion will likely be secondary.
Nevertheless, bad as congestion is today, it can only get worse as
international trade is projected to double within the next decade. Additionally, some trade flows within the
U.S. are projected to triple by 2020[5]. Such significantly increased demand for
transportation services will likely support higher freight charges; however the
overall policy goal must be to minimize transportation cost, thus contributing
to the U.S. general advantage from higher productivity.
Short sea shipping can
offer two potential benefits:
- SSS may be cost
competitive with overland shipping. To establish competitive costs, the
estimated costs of short sea shipping transport (including profit) must be
compared to the actual costs of overland shipping (also including
profit). In the most favorable
outcome, it will turn out that short sea shipping can be offered with a
higher profit margin than contemporary overland shipping. However, its success will alleviate
overland congestion, and thus would lower costs (increasing profits) in
the competing overland sector. Thus
SSS's success would contribute to improving its competitors' profit
margins. Producers cannot be
expected to choose short sea shipping unless it can be offered at rates
competitive with those offered by overland shippers, or lower.
- SSS may alleviate the
congestion/travel delay problem by bleeding off some of the cargo volume
from the highways. To some limited
extent, ability to realize this second benefit would justify policy
intervention even in the absence of any ability to achieve the first, and
studies should acknowledge and explore this possibility. However, it seems highly unlikely that
significant utilization of any alternative shipping facility would occur
unless it offers some clear benefit; e.g., of either cost or time
saving. If intermodal segments can
be identified where short sea shipping can offer a clear and significant time
advantage compared to overland transport, either around the clock or at
certain times of day, then SSS can be competitive even if its costs
require a higher price. However,
cost estimates must capture the cost of fuel consumption. The faster the operational speed of the short
sea shipping fleet, the more expensive to operate, the higher costs, and
the lower profits. Short sea
shipping can only prove viable if (a) its operating costs are sufficiently
low to enable pricing below overland shippers, or (b) it can match or
improve on the freight availability time offered by interstate
trucking. This includes travel time,
queuing, loading, and unloading, and in most cases should capture the fact
that deliveries made after normal business hours cannot be utilized or
processed by the customer until the start of the next business day. Though water-borne carriage is traditionally
slower than trucking, this advantage to trucking diminishes over weekends,
on overnight service, and increasingly at morning and evening rush hours
and other chokepoints. Operating
costs rise with ship speed, though to some extent, faster travel time
justifies higher pricing.
Exploratory modeling must capture the impact of both factors and
their interrelationship.
Short sea shipping may
offer both cost and time advantages, and to the extent possible, should be
implemented in a way which maximizes both advantages. Infrastructure should be designed with
significant excess capacity and with capability for expansion and flexibility.
Many maritime
professionals, government officials and academicians suggest that vessels with
speeds of 30 to 40 knots are necessary for short sea shipping to be competitive
with overland transport modes. This
conjecture must be carefully evaluated[6]. One of the cost advantages of ships over
trucks and trains (one figure cited is that ship transport is 23% less expensive[7]) is
lower fuel consumption, which depends on relatively low speed. Cost advantages and environmental benefits might
be erased if short sea shipping is implemented with a fleet of high-speed vessels.
The following cost
comparison may not hold at all or by as great a margin, for a high-speed
fleet. One 15-barge tow is equivalent to
870 trucks, according to the U.S. Maritime Administration's haul comparison[8]. Its energy consumption shows one gallon of
fuel can move one ton the following distances: 514 miles by inland barge, 202
miles by rail, and 59 miles by truck.
Part of this advantage disappears if the ships are operated at higher
speeds.
3. Quantifying Environmental Impact
This section quantifies
the environmental impact of a proposed short sea shipping service. North America's coastal and inland shipping
has largely been supplanted by railroad and interstate trucking, which are
often more expensive than ship movement, and frequently have greater
environmental impact[9]. Infrastructure costs for overland transport
have grown to the point where overland network infrastructure cannot easily be
expanded. Highway construction in the
U.S. costs approximately $32,000,000 per lane mile plus $100,000,000 per
interchange[10]. The
interstate highway system was originally authorized at 41,000 statute miles. To construct a parallel system of roughly
comparable extent, intended for trucks only, with two lanes in each direction,
would cost approximately $5,248,000,000,000.
This amount ignores interchanges and is nearly one-half the annual U.S.
GDP.
European Union data
document significant energy consumption advantages for maritime transport,
0.12-0.25 mega-joules/km as opposed to 0.60 for rail and 0.70-1.20 for
highway. CO2 emissions are
also lowest for maritime transport: 30g per ton/km versus 41g for rail and 207g
for highways[11]
(Commission of the European Communities 2001).
Becker, Burgess, and
Henstra (2004) and Lombardo, Mulligan, and Guan (2004) find high speed ships,
with their high fuel consumption and high environmental impact, would not be
feasible for SSS. Baird (2004) discusses
conditions for establishing economic feasibility of high speed operation[12]. Because harmful emissions are directly
proportional to fuel consumption, fuel consumption is a meaningful measure of
environmental impact. Based on a
conservative hypothetical baseline RoRo vessel with an 80 trailer capacity
(cost estimate data is presented in the appendix), fuel consumption is
estimated as a function of operating speed, estimated required shaft
horsepower, and Admiralty coefficient.
The Admiralty coefficient (Ac) is defined as a quadratic
function of the desired operating speed s
Ac
= 1.84 s2 - 139.96 s + 2791.50 (1)
Shaft horsepower (SHP)
is estimated as a function of the desired operating speed, deadweight capacity
d, and Admiralty coefficient
SHP
= (d2/3s3)/Ac
(2)
Substituting the
formula for Admiralty coefficient, we find that estimated SHP depends only on
design deadweight capacity and desired operating speed
SHP
= d2/3s3/(1.84 s2 - 139.96 s + 2791.50) (3)
The equation used to
estimate fuel consumption (F) over a round trip is
F
= (SHP x 2 x route length)/23.4s (4)
or, substituting the
expression for SHP in terms of s,
F
= (d2/3s2 x route length)/11.7(1.84s2 - 139.96s
+ 2791.50) (5)
This equation allows
us to estimate total fuel consumption at different operating speeds calling for
a range of different-sized engines, all over different route lengths. Table 1 provides insights
as to fuel
consumption measured in gallons given the operating speed in knots, over
route lengths ranging from 200 to 800 nautical miles, for operating speeds
ranging from 5 to 40 knots, for a hypothetical monohull RoRo vessel with a
capacity of 80 tractor-trailers. It
should be noted that fuel consumption is a linear function of the route
length. For example, at a given
operating speed, fuel consumption doubles if the route length is doubled, and
triples if the route length is tripled.
Table 1. Fuel Consumption as a Function
of Operating Speed and Route Length.
(Source: Lombardo, Mulligan, and Guan
2004. See note 13.)
|
Operating
speed |
Route length |
||||||
|
200nm |
300nm |
400nm |
500nm |
600nm |
700nm |
800nm |
|
|
5
kt |
17.23 |
25.84 |
34.45 |
43.07 |
51.68 |
60.29 |
68.91 |
|
10
kt |
93.47 |
140.21 |
186.94 |
233.68 |
280.41 |
327.15 |
373.88 |
|
15
kt |
299.64 |
449.45 |
599.27 |
749.09 |
898.91 |
1,048.73 |
1,198.55 |
|
20
kt |
809.01 |
1,213.52 |
737.10 |
921.37 |
1,105.64 |
1,289.92 |
1,474.19 |
|
25
kt |
2,080.53 |
3,120.79 |
1,957.27 |
2,446.59 |
2,935.91 |
3,425.22 |
3,914.54 |
|
30
kt |
5,330.56 |
7,995.85 |
10,661.13 |
13,326.41 |
15,991.69 |
18,656.98 |
21,322.26 |
|
35
kt |
12,283.46 |
18,425.19 |
24,566.92 |
30,708.66 |
36,850.39 |
42,992.12 |
49,133.85 |
|
40
kt |
17,190.52 |
25,785.78 |
34,381.04 |
42,976.30 |
51,571.56 |
60,166.82 |
68,762.08 |
|
Note: Fuel consumption in gallons of bunker fuel. |
|||||||
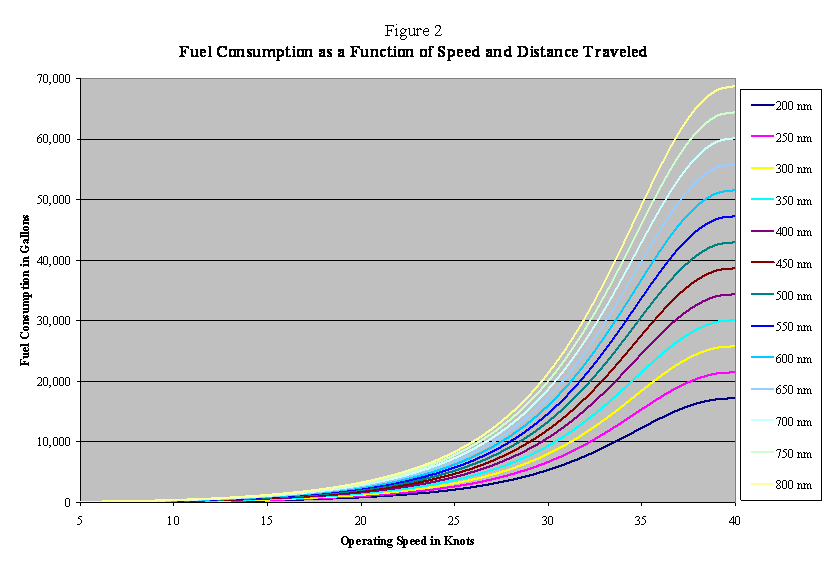
Fuel consumption
increases exponentially with the operating speed as shown in Figure 2; e.g.,
increasing operating speed by 50% increases fuel consumption by approximately
300%. This suggests that, in addition to
having dramatically heavier environmental impact, higher operating speeds
proposed by some SSS advocates will also impose dramatically greater
environmental impact and fuel costs.
To compare SSS with
overland trucking, the estimated fuel consumption per nautical mile traveled is
computed by this equation
F'
= (d2/3s2)/11.7(1.84 s2 - 139.96s +
2791.50) (6)
which is simply the
reduced expression for F (Equation 5) divided by the route length. Fuel consumption per nautical mile traveled
is independent of route length, and is an increasing function of speed, as
shown in Table 2.
Table 2.
Fuel Consumption per Nautical Mile Traveled and Fuel Economy as
Functions of Operating Speed.
(Source: Lombardo, Mulligan, and Guan
2004. See note 13.)
|
Operating
speed |
Fuel
consumption/nm |
Nautical
MPG |
|
5
kt |
0.09 |
11.6099 |
|
10
kt |
0.47 |
2.1397 |
|
15
kt |
1.50 |
0.6675 |
|
20
kt |
4.05 |
0.2472 |
|
25
kt |
10.40 |
0.0961 |
|
30
kt |
26.65 |
0.0375 |
|
35
kt |
61.42 |
0.0163 |
|
40
kt |
85.95 |
0.0116 |
|
Notes: 1. Fuel consumption/nm measured in gallons of
bunker fuel per nautical mile traveled. 2. Nautical miles per gallon compares roughly
to statute miles per gallon. 1 nautical mile = 1.15078 statute
mile. 1 statute mile = 0.86898
nautical miles. Exact conversion
requires knowledge of alternative sea and land routes under comparison. |
||
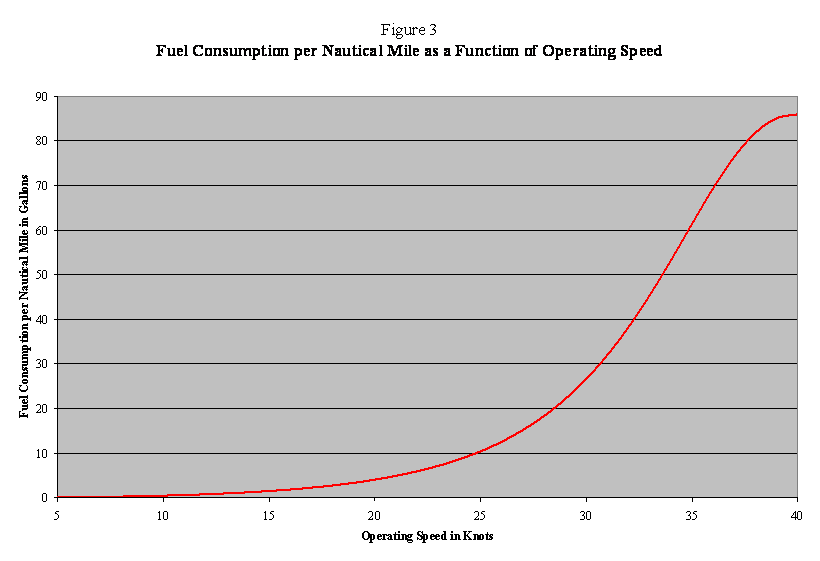
A single SSS vessel carrying 80
tractor-trailers at 20 knots will only burn approximately four gallons of
diesel fuel every mile (Table 2 and Figure 3).
This extremely modest level of fuel consumption has to be compared to
the fuel that would be burned, not by a single tractor-trailer, but by all
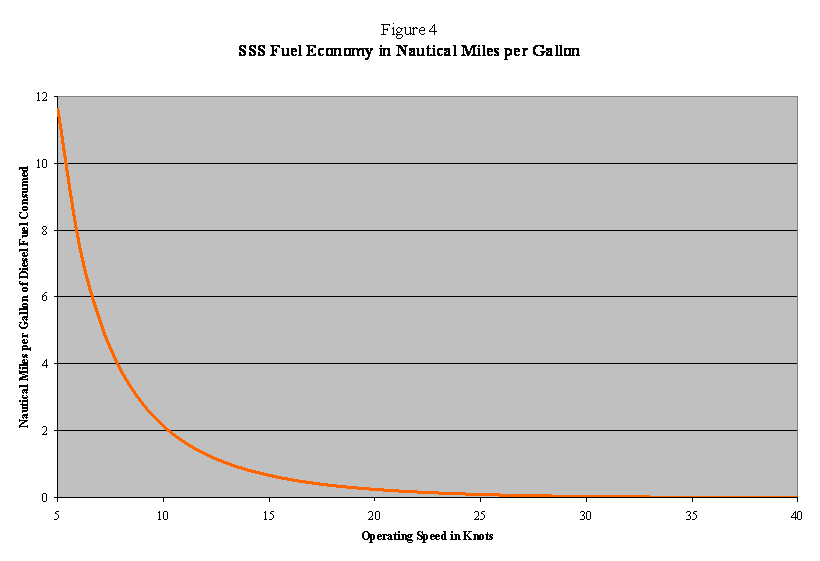
eighty. The reciprocal of fuel
consumption per nautical mile is miles traveled per gallon of fuel consumed
(Figure 4). These figures are also
provided in Table 2.
If a single tractor-trailer realizes fuel economy equivalent to four
miles per gallon, the eighty-trailer SSS vessel realizes the same level of fuel
consumption when traveling at only about eight knots. Although this is much slower, it must be kept
in mind that the 80 trailer RoRo ship is carrying eighty times the cargo of a
single tractor trailer. Thus, the ship
has better fuel economy and lower environmental impact as long as it operates
at a speed which allows for fuel economy better than 1/80 of the fuel economy
realized by tractor-trailers, which occurs at any speed below approximately 27 knots.
SSS can thus
contribute dramatically to improved
environmental quality. This improvement
in environmental quality is not limited to the superior fuel economy
characteristics SSS offers, but also results from the fact that reduced
congestion on interstate highways will allow truckers to drive faster and realize
better fuel economy. Furthermore, the
primary benefit is directly proportional to the number of tractor-trailers or
TEUs which can be removed from the interstate highway system and moved by ship.
4. Implications for Public Policy
Since SSS seeks to
address two critical problems outside the maritime industry, traffic congestion
and pollution, government subsidies may be justified, at least initially, as a
public policy initiative. In fact, due
to superior fuel economy, SSS can be implemented without subsidies, and
subsidizing SSS cannot, in and of itself, serve the public welfare. If private owners cannot earn profits
engaging in an activity, consumers do not sufficiently value that activity to
justify its performance. Various
restrictive regulations impose higher operating costs on U.S. domestic shipping
operators, which are passed on to consumers of transportation services. Frankel (2004) estimates U.S. cabotage policy
imposes $3 billion in direct costs, and an additional $6 billion in indirect
costs, on the U.S. economy[13]. Environmental benefits justify reevaluating
restrictive government regulation and weighing costs versus benefits.
There remain other
spheres where the government can play a financial role. The government can utilize SSS as a customer,
taking advantage of cost savings and lowered environmental impact. The government can utilize SSS to move the
mail, defense equipment, and military units, bypassing potential bottlenecks in
overland transportation networks. The
government can create a tax environment favorable to SSS operators and their
customers, including but not limited to, permitting accelerated depreciation,
tax rebates, and tax cuts. An effort
should be made to implement favorable tax treatment for freight service
consumers in terms of granting tax rebates to users of SSS.
Because overland shippers, the potential customers of SSS, pay
significant taxes and use fees, mostly to state governments, part of these
taxes can be rebated. The government can
rebate fuel and vehicle use taxes to SSS customers, to reward them for reducing
pollution and relieving congestion by switching from overland carriage. Every mile a truck is carried over the SSS
network translates roughly into one less mile traveled over the interstate
highway system, with attendant reductions in fuel consumption and environmental
impact. Rebating highway and fuel taxes
rewards truckers who utilize SSS for the role they would be playing in mitigating
environmental impact, as well as lessening the congestion experienced by other
truckers and personal autos using the interstate highways. SSS can offer significant environmental
benefits, which justifies some level of tax relief or other government
incentives.
5. Conclusion
The challenge facing short
sea shipping is to develop a commercially viable business model for the Western
Hemisphere and an enhanced business model for Europe. The critical
success factor for SSS is that it must facilitate cargo movement as an
inexpensive, seamless component of an integrated, intermodal transportation
system. Alleviating the environmental degradation forced by a growing
economy and population will be a significant side benefit. Key considerations for implementing SSS include:
- Short sea shipping
will not develop automatically as the panacea for reducing highway
congestion and improving the natural environment.
- Short sea shipping may
contribute to achieving these goals if companies develop a niche or focus
strategy and target those transportation routes that will most clearly and
significantly benefit from the water movement of cargo.
- Shipping firms should
form partnerships with overland carriers and large consumers of transportation
services.
- Short sea shipping
companies may build market share initially by forming strategic alliances
with trucking companies who already ship a portion of their cargo via sea.
- Public policy can
subsidize SSS directly, but providing significant tax benefits will likely
prove of greater financial benefit to SSS providers, as well as reward
consumers of transportation services for selecting the most
environmentally benign transport mode.
The technical data on
estimated fuel consumption and fuel economy contained in this report can be
used to educate public policy decision makers, environmentalists, and maritime
industry professionals who need to develop a sophisticated understanding of SSS
and its implications for preserving the environment. The favorable appraisal of SSS's environmental
impact suggests the concept will inevitably become a reality. A successful short sea shipping program
offers an opportunity to add value to a national or international
transportation network and thus improve economic efficiency and ultimately the
societal standard of living.
Appendix: Basic
ship cost estimate
The basic estimation
methodology is due to Benford (1965, 1967) and Hunt and Butman (1995)[14]. The ship construction estimate starts with an
assumed cargo size t, which in this case, is 80 tractor-trailers, each hauling
standard 40 foot, two-TEU trailers on chassis.
The ship’s design deadweight capacity d is estimated as
Deadweight
capacity d = 28.6t (A1)
The ship’s length is
estimated as
L
= 240.17 + 0.1107d
(A2)
Beam is estimated as
B = 88.315 – 0.0226L
(A3)
Depth of the ship,
keel to gunwale height, is estimated as
D
= 14.19 + 0.0255L
(A4)
Draft of the ship T,
the part of the ship’s depth below the waterline, is estimated as
T
= 8.8585 + 0.047B
(A5)
The Admiralty coefficient
Ac, is a quadratic function of the ship’s operating speed s
Ac
= 2791.5 - 139.96s + 1.84s2 (A6)
This enables us to
estimate the required shaft horsepower SHP for the engines given deadweight
capacity and Ac
SHP
= 0.667(DWT)3/Ac
(A7)
Cubic number, a
measure of the hull volume or capacity, is a function of length, beam, and
depth
CN
= LBD/100
(A8)
The steel weight for
the hull in long tons is estimated as
WH
= 280(CN)0.9(0.675+ 0.5 + 0.7)(1 + 0.36 x 0.05 x LS/L)(0.00585
x (L/D – 8.3)1.8 + 0.939)
(A9)
In this formula, the
ratio LS/L, the ratio of the length of the ship's superstructure to
the overall length of the hull, will be assumed to be one.
Then, the steel weight
of the ship’s outfit is estimated from
WO
= 25(CN/100)0.825 (A10)
The steel weight for
hull engineering is estimated from
WHE
= 43(CN/1000)0.825 (A11)
The steel weight of
the engine and related ship’s machinery is estimated as
WM
= 60(SHP/1000)0.50 (A12)
Then the ship’s
estimated displacement is the sum of the steel weights and the deadweight
capacity
Disp
= d + WS + WO + WHU + WM (A13)
We assume a standard
U.S. shipyard hourly labor rate of $16.50 because under the Jones Act, all SSS
tonnage will be built in American shipyards, though allowing foreign
competition would greatly lower the cost of ship construction.
Labor hours required
for fabrication and construction are estimated from the equations given in the
following table.
Table A1. Labor Hour Estimation Formulae by Ship
Component.
Source:
Developed by authors.
|
Component |
Formula |
|
Hull |
|
|
Outfit
|
MHO
= 20,000(WO/100)0.90 |
|
Hull engineering |
MHHE =
5,100(WHE/1000)0.75 |
|
Machinery |
MHM =
25,000(SHP/1000)0.60 |
Then the total cost to
complete that component of the ship is given by the following equations.
Table A2. Total Cost by Ship Component
Material plus Labor Cost. Source:
Developed by authors.
|
Component |
Formula |
|
Hull |
CH =
1800WH + $16.50(MHH) |
|
Outfit |
CO =
14000WO + $16.50(MHO) |
|
Hull engineering |
CHE =
27000WHE + $16.50(MHHE) |
|
Machinery |
CM =
6000WM + $16.50(MHM) |
Total construction
cost is simply the sum of the material and labor costs for each category, with
120% shipyard overhead added. Thus the
total labor and material costs are multiplied by 2.20.
Cost
= 2.20(CH + CO + CHE + CM) (A14)
Shipyard profit is
estimated at 10% of the cost to the builder, so the price charged to the owner
is 10% higher than the shipbuilder’s cost.
Due to financial and risk issues, the owner’s cost is assumed to be 5%
higher than the actual price charged by the shipyard.
Owner’s
cost = 1.05(1.10(2.20(CH + CO + CHE + CM))) (A15)
Days per trip is
computed as twice the route length, for a round trip, divided by the operating
speed times twenty-four hours. One day
is arbitrarily added for turnaround time in port, which is a highly conservative
assumption for SSS RoRo service. Actual
turnaround time should generate significant additional economies.
Days/trip
= (2 x route length/speed x 24) + 1 (A16)
Fuel expenses are the
price per gallon of bunker fuel, then multiplied by the ship’s shaft horsepower
times 0.33 times twice the route distance, divided by the speed, divided by 7.8:
Fuel
cost = $bunkers(0.33SHP(2 x route length/s)/7.8) (A17)

