A Forecast of U.S. Real Gross Domestic Product for the Year 2010, Based on the Growth of Consumption and Population
 
JOSH ROPER and DEBRELL GARY
College of Business
Western Carolina University
 
Abstract
 
U.S. real GDP is forecast to grow to approximately 9044.6 billion dollars in the year 2010. This forecast is based on the Keynesian aggregate expenditure model assuming government spending, investment, and net exports increase at a constant rate over these years. The explanatory variables used in the forecast were consumption and population. Consumption for the year 2010 is projected to be approximately 6202.7 billion dollars, and population is projected to be 297.2 million people. The information for GDP, consumption, and population is taken from actual annual data from 1983-1998. U.S. Census Bureau population projections are used to forecast consumption and GDP up to 2010. With a growing population, GDP and consumption are forecast to grow steadily over the twelve year forecast horizon. This is indicative of a strong economy, requiring no government intervention during this period. (JEL: E12, E21)
 
Part 1. Introduction
 
This paper forecasts U.S. real gross domestic product (GDP) up to the year 2010. The explanatory variables are real personal consumption expenditures and population. The forecast approach is based on the Keynesian aggregate expenditure model, assuming as consumption increases, so does real GDP. The approach uses annual values for GDP, consumption, and population from actual data from 1983-1998, as well as using estimates of consumption and population for the years 1999-2010. The Kenynesian approach offers simplicity in use, and focuses mainly on the effect consumption has on the level of national output. This forecast also assumes the other variables of the aggregate expenditure model, government spending, investment, and net exports, continue to increase at a constant rate.

Since the population of the U.S. is continually increasing, and consumption is a major component of GDP, it is important to understand the relationship among these variables. Also, since the forecast is a considerable amount of time into the future, the probability of accuracy leaves a wide margin for error.

The rest of the paper is organized as follows: Part 2. presents the data used to forecast GDP, consumption, and estimates of the population; Part 3. presents the theoretical basis for the approach taken in forecasting GDP; Part 4. presents the forecast for GDP, the two variables, and the methods used in determining these values; Part 5. evaluates the importance of these projections for the economy; Part 6. discusses the conclusions for economic policy.
 

Part 2. Data
 
The information for both U.S. real GDP and consumption for the years 1983-1998 were taken from the Federal Reserve Bank of St. Louis Federal Reserve Economic Data (FRED), which are FRED variables GDPC92 and PCEP92 respectively. The data for the population is historical data given by the U.S. Bureau of the Census for the years of 1983-1997. The population data for 1998-2010 are estimates made by the Bureau. Both GDP and consumption are measured in billions of chained 1992 dollars at seasonally adjusted rates. Population is measured in millions.

The Bureau of Economic Analysis and the Census Bureau, U.S. Department of Commerce, are the primary sources of the data. The sample period for the data is 1983-1998. The forecast horizon is twelve years into the future. The data was chosen for the forecast because the information is the actual historical values of the variables, recorded by the appropriate government authorities.

Real GDP is the sum of consumption expenditures, investment expenditures, government expenditures, and the total of net exports less net imports. This is show by the aggregate expenditures model where AE = GDP = C + I + G + X. Since consumption is a major component of GDP, it is useful to understand the effect it can have in determining GDP. However, consumption is just one of the variables that can be used to forecast GDP. Any one of the components of the aggregate expenditure model can be used in determining GDP based on the Keynesian theory. Government spending, investment, and net exports can be used as a linear function in determining GDP, assuming the rest of the variables remain constant. It is important to note that although all of the variables can fluctuate independently of one another, fluctuations in GDP result from fluctuations of all the other variables.

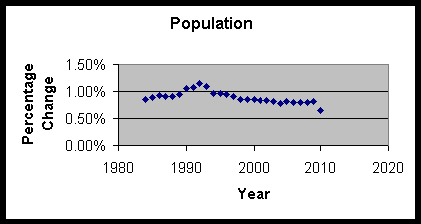
Graph 1 shows the percent change from the year to year forecast by the Census Bureau. Notice population is estimated to increase at a decreasing rate in the future. This is important to note in determining the effect this will have on consumption in the future.
 

Graph 1
 

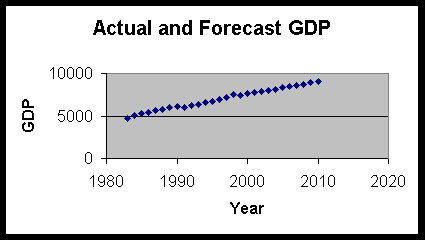
Graph 2 shows the changes of actual GDP and Forecast GDP.
 

Graph 2
 
Graph 3 shows actual per capita GDP and forecast per capita GDP.
 
Graph 3
 
Part 3. Economic Theory:
Consumption and Population as a Function of Real GDP
 
This forecast assumes growth rates of government spending, investment, and net exports will remain constant over the next twelve years. The level of real consumption spending is used to predict the level of real GDP each year. The relationship is GDP = AE = C + G + I + X, where government spending, investment, and net exports remain constant, and population determines consumption. This relationship is shown in the following equation where Y represents GDP:
 
Y = f(C, Pop.)
 
This theoretical approach is appropriate to forecast GDP because output is known to be a function of population, for example through the work force, which is responsible for producing output, and funding consumption. This is a positive relationship where when population rises so does consumption, and then in turn increases the level of GDP.
 
Part 4. Forecasts for GDP and Consumption

The equation used to estimate consumption for the year 2010 was done by an ordinary least squares regression formula for the years 1983-1998. The data input was actual population and consumption for these years. The R-squared of the estimate is 0.970. This indicates that approximately 97% of the variations in population are explained by the variation of consumption. The regression estimate is (t-statistics in parentheses):

C = -7022.66(-13.38) + 44.5002(21.31)(population)
 
The equation used to estimate GDP for the 2010 year was also done by an ordinary least squares regression formula for the years 1983-1998. The data input was actual GDP and consumption for these years. The R-squared of the estimate is 0.998. This indicates that approximately 100% of the variations in consumption are explained by the variation of GDP. The regression estimate is (t-statistic in parentheses):
 
GDP = 257.006(4.07) + 1.416722(93.86)(consumption)
 
Based on the estimates of the equations, consumption for 2010 will be 6202.7 billion chained 1992 dollars, based on the Census Bureau population projection of 297.2 million people. This figure is then used in the second equation to determine forecast GDP. The estimate of the second equation, with the consumption value, forecasts GDP for the year 2010 to be 9044.6 billion chained 1992 dollars.

Table 1 shows the forecasts for GDP, consumption, and population for the forecast period.
 

Table 1
Forecast GDP, Consumption, and Population
for 1998-2010*
Year
GDP
% change
Consumption
% change
Population
% change
1998
7549.9
5.02%
5151.2
5.83%
270.0
0.83%
1999
7474.8
-0.99%
5094.7
-1.10%
272.3
0.85%
2000
7619.8
1.94%
5197.0
2.01%
274.6
0.84%
2001
7764.8
1.90%
5299.4
1.97%
276.9
0.84%
2002
7909.8
1.87%
5401.7
1.93%
279.2
0.83%
2003
8054.8
1.83%
5504.1
1.89%
281.5
0.82%
2004
8193.5
1.72%
5602.0
1.78%
283.7
0.78%
2005
8338.5
1.77%
5704.3
1.83%
286.0
0.81%
2006
8483.5
1.74%
5806.7
1.79%
288.3
0.80%
2007
8628.5
1.71%
5909.0
1.76%
290.6
0.80%
2008
8773.5
1.68%
6011.4
1.73%
292.9
0.79%
2009
8924.8
1.72%
6118.2
1.78%
295.3
0.82%
2010
9044.6
1.34%
6202.7
1.38%
297.2
0.64%
*GDP and consumption are measured in billions of chained 1992 dollars,
and population is measured in millions.

As shown in Table 1, population and consumption are increasing each year, with the exception of 1999. As the equations show, GDP follows the same pattern as the two variables, and is also increasing for the forecast years with the exception of 1999. The negative change in 1999 does not imply a recession for the year. When using ordinary least square regression the forecast is a linear function, and the negative shift is a result of the calculation. It is an artifact of the regression estimate which occurs whenever positive regression residuals are found for the last period of the regression.

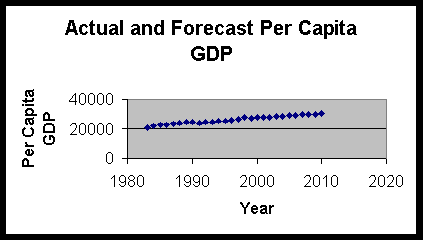
Another important item of information is per capita real GDP. Per capita real GDP is the amount each consumer will contribute to real GDP on average. As shown in Table 2, per capita GDP is rising for the forecast horizon.
 

Table 2
Forecast Per Capita GDP for 1998-2010*
Year
Per Capita GDP
% change
1998
27962.6
4.1%
1999
27450.6
-1.8%
2000
27748.7
1.1%
2001
28041.9
1.1%
2002
28330.2
1.0%
2003
28613.9
1.0%
2004
28880.9
0.9%
2005
29155.6
1.0%
2006
29426.0
0.9%
2007
29692.0
0.9%
2008
29953.9
0.9%
2009
30222.8
0.9%
2010
30432.7
0.7%
* Per capita GDP is measured in thousands of chained 1992 dollars.
 
Part 5. Forecast Implications

GDP is important to forecast because it indicates the nation’s output for a given year. The forecast of increasing GDP indicates economic activity will grow steadily in the future. Along with a growing economy, certain economic needs can be determined. There will be a growing need for labor services, leading to a lower unemployment rate if the labor force grows more slowly than GDP. Lower unemployment and increased demand for labor will increase consumer income, which may increase the marginal propensity to consume.

With higher demand for consumer goods and services, manufacturers can use these trends to estimate inventory needed to maintain the levels of consumption. Depending on the predicted outcome, surpluses and shortages can be avoided. This also allows businesses to maximize the cash flow provided by current resources. These trends can also help determine the level of employment needed, decreasing business expenses.

The fact that per capita real GDP is forecast to increase up to 2010 indicates an increase in real income, real wealth, and a rising standard of living, for the U.S. throughout the forecast period.
 

Part 6. Policy Conclusions
 
Real GDP is forecast to be approximately 9044.6 billion dollars in the year 2010. This is a 20% increase from 1998. This value is based on the forecast of consumption to be 6202.7 billion dollars, and population to be 297.2 million people.

A rise in real GDP will affect all sectors of the economy. The individual sectors will have to anticipate consumer demand for their particular area, and plan accordingly. Determining the changing demand of consumers will help companies adjust to these changes in the areas of production and employment. This will be helpful in evaluating when to increase or decrease production, and when more or less employment is needed to fulfill these requirements.

This forecast assumes government spending will remain a constant fraction of real GDP during the forecast period. For now, the government should not change any of its policies. The forecast predicts the economy will remain strong well into the future. However, if the economy becomes stagnant the government may want to intervene in order to stimulate the economy as needed.
 

Reference