A Two-year Forecast of U.S. Industrial Production
based on the Keynesian Investment Function

AMBER HEAD and MINDY HOVIS
College of Business
Western Carolina University

Abstract

U.S. industrial production output is forecast to increase steadily in the next two years (2000-2001).The forecast is based on a Keynesian aggregate expenditure model.The explanatory variable is the 3-month T-bill interest rate.The results from the forecast imply U.S. industrial production output will continue to increase throughout 2000-2001.If the forecast comes to pass, the affected industries need to be prepared to operate at full capacity and possibly increase their production levels.If affected by the capacity utilization rate, the industry aims to reach a maximum profitability through maximum output.The Federal Reserve should continue to keep prices and interest rates as stable as possible.(JEL: E22, E66)

 

Part 1. Introduction

This paper forecasts U.S. industrial production output for the years 2000-2001.The explanatory variables are lagged interest rates.The approach is based on the Keynesian Aggregate Expenditure Model using the investment function.The Keynesian approach exploits the role of private investment expenditures in driving aggregate economic activity.

Real GDP is the most comprehensive measure of national income and output; therefore, the affects of industrial production output will effect GDP.Continued growth in industrial production output helps to sustain low unemployment and a rising standard of living.For example, if the forecast predicts a downturn of industrial production output, this would in turn predict a recession.The forecast horizon of two years was chosen to minimize the possibility of external factors impacting the economy in an unforeseen way.The forecast horizon is short enough to avoid seriously overstating or understating future industrial production.

The rest of this paper is organized as follows: part 2 presents the data used to forecast U.S. industrial production output; part 3 presents the theoretical basis of the Keynesian Aggregate Expenditures Model; part 4 presents forecasts of U.S. industrial output for 2000-2001; part 5 evaluates the importance of the forecast for the economy; and part 6 discusses conclusions for economic policy.

Part 2. Data

All variables are taken from the Federal Reserve Economic Data (FRED), the Federal Reserve Bank of St. Louis. The observation interval is monthly.The interest rate data are the secondary market 3-month T-bill rates given in FRED variable TB3MS.The sample period for the variable was from January 1990 through January 2000.The forecast horizon is two years into the future.The regression of interest rates on industrial production output was done by using a basic model for regression.

Using interest rates (which is part of real GDP) enables an appropriate forecast of U.S. industrial production output.The reason it is best for this forecast is because the Keynesian model depends strongly on the consumption behavior of households and the investment behavior of private firms.The 3-month T-bill was used because the Fed is the primary buyer and holder of U.S. Treasury securities, and which also strongly influences market interest rates.As a result of the Fed buying U.S. Treasury securities, money is put into circulation.With the amount of money in circulation increasing, the public makes more purchases, causing U.S. industrial production output to increase.

Part 3. Forecasting with the Keynesian Aggregate Expenditures Model

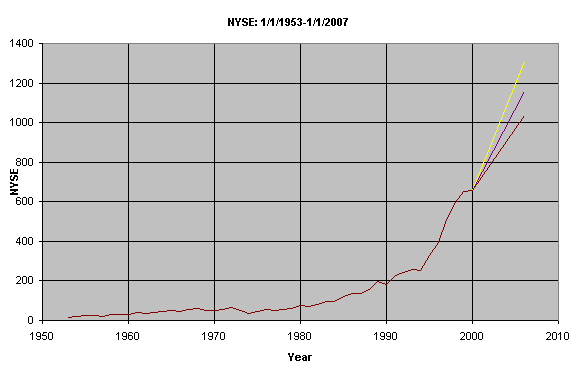
The Keynesian model shows that interest rates affect investments, which in turn effects GDP.Figure 1shows that as interest rates decline, investments began to rise.As investments began to rise, GDP in turn rises since investment is a function of GDP.As a result of interest rates declining it causes the U.S. industrial production output to rise.If the interest rate rises, investments begin to decrease which causes GDP to decrease along with decreasing U.S. industrial production output.The Keynesian Aggregate Expenditure Model is written as:

 

Y = C + I + G + NX

The Y identifies GDP, which consists of consumption (C), investment (I), government spending (G), and net exports (NX). The investment function as a part of the Keynesian identity is shown in the following equation:
I = f (r)

Along with the investment function, GDP depends on interest rates.However, investments are not dependent of GDP.Therefore, the investment function and GDP have their separate equations based on interest rates.The investment function, based on interest rates, was shown above.GDP as a function of interest rates is shown below:

Y = f (r)

This forecast assumes the interest rate will average 4.855455 percent for the next two years, based on the data from the past ten years (1990.01-2000.01) and will have an impact on investment spending and GDP.The interest rates will be used to project output into the future for the next 24 months of 2000-2001 to provide a short-term projection of U.S. industrial production output.The values for projected U.S. industrial production output was calculated using this equation:

Yt = f(Yt-2, rt-2), (1.

This is a simple model appropriate for forecasting short-term U.S. industrial production output.The forecast should be interpreted as a trend of U.S. industrial production output in the absence of a recession.This model is probably not adequate to forecast a recession, especially one caused by unanticipated real aggregate supply shocks.

Part 4. Estimates of the Investment Function and Forecast of Industrial Production Index

U.S. industrial production output is used to proxy GDP.Since the investment function of GDP is affected by interest rates, GDP will in turn be affected.As interest rates increase, investments, along with consumption will decrease.The decrease of investment and consumption due to rising interest rates causes less demand in U.S. industrial production output.Therefore, the results of the forecast show that U.S. industrial production output is dependent on interest rates, which in turn will have an effect on GDP.

 
Table 1
Regression Estimate of U.S. Industrial Production Index Forecasting Equation 1: 1990.01-2000.01
Explanatory Variable
Estimated coefficient
t-ratio probability level
Intercept
-4.51
0.0587
Lagged U.S. Industr. Prod. Index
1.20
0.0
Lagged Interest Rates
-1.70
0.0
R2 = .9745
F (zero slopes) = 1798.061
Prob F = 0.0

 
R-squared is .9745.Since the R-squared is considerably close to one, this regression analysis can be determined as a sufficient forecast. The probability level of the F-statistic is considerably low (1.22E-75) which tells us to reject the null hypothesis.To explain this in English, this means the forecasted data is acceptable and there is no reason to consider this forecast to be an insignificant hypothesis.The coefficients used in determining our regression analysis were lagged U.S. industrial production output and lagged interest rates.Considering the estimated coefficient of the lagged interest rate is–1.7011, this shows that interest rates are slightly declining in the future.On the other hand, as interest rates are declining, U.S. industrial production output is rising.The estimated coefficient of lagged U.S. industrial production output is 1.2023, which suggests future output will continue to rise.The equation below gives an illustration for the month of February in the year 2000:
Y2000.02 = -4.5082+1.2023x (130.738) - 1.7011x (5.09) = 144.0135.

Overall, the regression analysis forecast future interest rates to decline, which causes U.S. industrial production output to rise.Considering the U.S. industrial production output has a monthly growth rate of 1.5 percent, this forecast is fantastic.

From the estimation provided by the regression, a target forecast is determined for the future months beginning at 2000.02 up through 2002.01.Table 2 outlines the forecast data.


 

Table 2 
Projected U.S. Industrial Production Index
Month
Output
2000.02
144.01
2000.03
144.52
2000.04
145.35
2000.05
146.20
2000.06
145.09
2000.07
144.89
2000.08
147.76
2000.09
148.20
2000.10
149.98
2000.11
148.82
2000.12
148.88
2001.01
149.27
2001.02
149.65
2001.03
150.41
2001.04
151.06
2001.05
151.60
2001.06
151.99
2001.07
152.89
2001.08
153.05
2001.09
153.51
2001.10
154.40
2001.11
154.58
2001.12
155.09
2002.01
156.54

 
If the forecast target actually comes to pass, it will be a good thing.This forecast implies 1.5- percent monthly growth in U.S. industrial production output.The effects of this forecast would require industries to be prepared to operate at full capacity and possibly increase their capacity levels.Below, figure 2 illustrates the growth in the projected output.


 

In Figure 2, the current interest rates (blue line) along with current U.S. industrial production output (purple line) are provided. The current variables are shown over a period of ten years (1990.01-2000.01). With this data, along with the use of regression tools, the forecast for U.S. industrial production output is derived (yellow line). Therefore, we placed the target U.S. industrial production output line in the first two years of the past ten years’ data. If adequate resources were available, the target U.S. industrial production output line would have been placed in the two years following the past ten years’ data (2000.02-2002.02).

 

Part 5. Forecast Implications: “Pink Hearts and Red Roses”

The forecast appears favorable to the manufacturing industry.According to the forecast, industrial production output is on a continuous rise with an occasional downfall.However, the downfall will eventually pick back up and get in the rising pattern.The recommendation for industries is to continue taking orders to operate at full capacity because the industrial output will be productive in the future.

Part 6. Policy Conclusions

U.S. industrial production output is projected to rise for the next two years with an occasional slight downfall.If the forecast comes to pass, the affected industries need to be prepared to operate at full capacity and possibly increase their capacity level.Affected industries may include those of the industrial, technology, and service sectors.The best way to describe industrial sectors is “enterprise diligence,” which includes the highly developed manufacturing companies.Technology on the other hand, which is known as “computer whiz,” provides for the accomplishment of a task using technological methods of knowledge.The “public servant,” known as the service sector, is defined as the performance of official or professional duties to provide a benefit or assist a customer.For example, a firm of the technology sector may need to make technological advances to efficiently meet future quotas. Overall, the government and the Federal Reserve should make any changes because this forecast is based on the past two-years of interest rate data.For the past two years the economy has been running efficiently; therefore, the government and Federal Reserve should leave things as they were two years ago.

References

Federal Reserve Bank of St. Louis, Federal Reserve Economic Data (FRED) (1-21-00), http://www.stls.feb.org/fred/

(02-21-00).