An
Empirical Examination of Austrian Business Cycle Theory
ROBERT F. MULLIGAN
"There can never be a scarcity of currency except when there is too
much of it."
William
Graham Sumner 1891 I: 188.
Abstract. A vector error-correction model (VECM) of
real consumable output is identified and estimated, employing the
Johansen-Juselius (1990) test for cointegration. Because the Austrian school views economic
activity as a disequilibrium process, VECM estimates offer an empirical methodology
especially amenable to interpretation through Austrian business cycle
theory. Austrian business cycle (ABC)
theory was pioneered by Ludwig von Mises (1912, 1949) and Friedrich Hayek
(1933, 1935, 1941). Harwood's (1932)
account of the business cycle is very similar.
ABC
theory focuses on credit expansion, which artificially lowers interest rates
creating an investment boom and unsustainable business expansion. ABC theory is presented prominently by
Haberler (1937) as a leading modern theory of the business cycle, and yet has
largely fallen out of favor with orthodox economists. This is especially surprising because only ABC
theory can claim much success in providing coherent and plausible explanations
of historic business cycles.
Rothbard
(1963) explains the Great Depression in terms of ABC theory, concluding that
overexpansion of the money supply in the late 1920s caused the stock market
crash, and exceptionally unskilled policy responses created the prolonged
secondary contraction by preventing the economy from liquidating the
accumulated malinvestment and unemployment.
Although their explanation of the dynamics of the depression differs and
is distinctly non-Austrian, Friedman and Schwartz (1963) agree that bad policy
greatly exacerbated what would have been an unexceptional recession.
Garrison's
(2001) restatement of ABC theory and his applications to historical cycles
should lead to renewed interest in Austrian capital theory. According to ABC theory, recession constitutes
the process of liquidating resources and production plans misallocated during
the unsustainable boom. This finds
compelling evidence of such cycles of malinvestment and liquidation in
1959-2003 U.S. data.
Key
words: Austrian business cycle theory, Hayekian triangle,
Error-correction model
JEL
classification: B53, C32, E23, E32, E43.
1. Introduction
Austrian
capital theory (Mises 1912, 1949; Hayek 1931; subsequently developed by Hayek
1933, 1939, 1941) is used to construct and interpret a vector error-correction
model estimated with
Whenever interest rates rise, higher rates of return
in production are necessary to compete with financial instruments, such as
relatively higher-yielding government bonds.
This is manifested in a shifting of resources away from early stages of
production to later stages, and can be shown as a shortening of the base of the
Hayekian triangle (Figure 1) (Hayek 1931:39).
This paper explicitly tests the main assertion of Austrian business cycle
theory, that lowering the interest rate lowers real output.
The
rest of the paper is organized as follows.
The theoretical basis for the paper is briefly developed in section
2. Section 3 discusses some applications
of Austrian business cycle theory in the economics literature. Data sources are documented in section
4. Section 5 develops the methodological
approach applied in section 6. Section 6
presents and interprets the empirical work, consisting of an error-correction
model of real output as measured by real consumption expenditures. This section
presents tests for cointegration followed by estimates of the error-correction
model. Concluding comments are presented
in section 7.
<<Figure
1 about here.>>
2. The Austrian Theory of the Business Cycle
Consider the problem faced
by a capitalist with idle savings to invest, who engages in a specific
productive activity. One use of these
idle savings is to purchase intermediate inputs or goods-in-process, adding complementary
resources such as labor and capital services to raise the sale value to another
capitalist who engages in the next stage of production. The capitalist's decision focuses on their
opportunity cost, the prevailing interest rate which could be realized by
lending the savings to someone else.
Capitalists opt for their own productive activity if the return is
higher than could be realized through lending, and lend out the savings if the
market interest rate exceeds the return to their own production. Thus, if the interest rate falls, less money
will be lent out and more will be used to finance productive activities, and
vice versa.
At the same time, however,
the interest rate influences consumers' decision on how to divide their income
between consumption and saving. The
lower the interest rate, consumers save less and consume more. Any lowering of the interest rate must
simultaneously increase consumption spending, lowering saving, as well as
increase investment in productive activities.
This process would work in reverse when the interest rate rises, if
productive activities could be liquidated rapidly and at low cost.
When the interest rate
rises, capitalists should liquidate their own productive activities to the
extent possible, and lend the money out to take advantage of the higher
return. Ideally, the opposite should
occur when interest rates fall. However,
physical capital comprises illiquid assets, and once savings is invested in
productive activities, it cannot be extracted without delay and loss of
value. Once a capitalist invests in
productive equipment, a higher interest rate may make it desirable to lend out
the money that could be raised by selling the equipment. The sale may involve a delay, however, and as
long as the capitalist enjoys a comparative advantage in the productive
activity, the equipment's selling price must be below what the equipment was
worth to the capitalist.
This cost asymmetry in
converting between financial and physical capital is the basis for Bischoff's
(1970) "putty-clay" model of investment. Uninvested "putty" capital, also
called financial capital, is highly liquid, and can easily be moved from loan
markets into productive activities. Once
savings is tied up in installed physical or "clay" capital, it cannot
be moved costlessly from productive activities back into loan markets, or even
into alternative productive activities.
The Austrian school emphasizes these costs associated with adjusting the
capital structure – also called the structure of production – when interest
rates rise, though it should be kept in mind that similar adjustment costs are
incurred whenever labor, human capital, and raw materials are reallocated. Installed capital equipment can be thought of
as the least adaptable input and the one that most often constitutes a binding
constraint on the process of reallocating production in response to increases
in the interest rate.
In the Austrian view, the
prosperity which precedes a recession is marked by overexpansion of the money
supply above what could be justified by any increase in real consumable output
or productive activities. This could be
seen through a growth of the money supply greater than the growth of real
output, particularly of real consumable output, which unlike investment
spending, is used directly to satisfy individuals' wants. It can also be seen through a lowering of the
nominal interest rate below an appropriate, sustainable, equilibrium interest
rate which would prevail in the absence of monetary overexpansion. While the interest rate is artificially
depressed during the expansion phase, firms invest intensively in physical
capital. Since the interest rate is so
low, the production process can take more time to produce the same amount of real
consumable output, so the production process becomes more drawn out, or more
roundabout, and the slope of the hypotenuse of the Hayekian triangle becomes
flatter, as its base becomes longer.
At the same time, however,
the lower interest rate means consumers save less of their income and consume
more. The below-equilibrium interest
rate results in an economy which takes longer to produce real consumable
output, but also ensures consumers are less willing to wait for their wants to
be satisfied. This production structure
is unsustainable, and must result in abandonment of much capital installed in
early stages of production, and many entrepreneurial plans, as well as high
labor unemployment, even if the interest rate is kept low. Entrepreneurial plans of both producers and
consumers are disrupted because they were predicated on a lower interest rate
and a longer production structure.
In Austrian business cycle theory, the onset of a
recession can occur in any of three ways:
(1) Deflation:
Often, following overexpansion of the money supply, the monetary authorities
will recognize the dangers of the low interest rate and will intervene to
effect adjustment by tightening the money supply. This is signaled by higher interest rates
toward the end of the expansion and the early stages of the recession. This policy response results in a
shorter-lived, though usually more severe, recession, which is the process of
the economy bringing the production process back in line with the sustainable
interest rates and actual time preference.
Contractionary policy can be observed most notably preceding the onset
of the Great Depression, the Volker recession of 1981-82 and the 2001
recession.
(2) Steady inflation: The monetary authorities
continue to inflate the money supply at approximately the same rate as during
the expansion. This would normally occur
whenever the monetary authorities remain unaware of the ill-advised aspects of
their policy-induced credit expansion, or are otherwise innocent of economic
theory. As low interest rates persuade
entrepreneurial managers to invest more in early stages of production and
lower-yielding productive activities, and simultaneously persuade consumers to
save less and consume more, the need for complementary resources required to
simultaneously increase the resource allocation in both early and late stages
of production becomes critical.[1] Demand for credit finally outstrips the
monetary authority's intended oversupply, driving interest rates up, leading to
massive abandonment of production plans and lower-yielding capital equipment,
precipitating higher unemployment. Most
postwar recessions have started this way, including the first Gulf crisis
recession of 1990-91.
(3) Accelerating inflation: Finally, the monetary authorities may foresee
the recession, or perceive the increased demand for credit, and attempt to
forestall the collapse by increasing the money supply even faster. The economic collapse can be postponed as
long as the monetary expansion proceeds faster than rational individuals can
revise their expectations. This course
of policy is inevitably rendered fruitless as market participants must
eventually learn to anticipate future inflation. This strategy of accelerating inflation may
delay the onset of a recession, but guarantees a more severe and protracted
one. This experience characterized the oil-shock
recessions of 1969-70 and 1973-74.
Productive resources have differing degrees of
substitutability and complementarity (Garrison 1985:168; 2001:49). ABC theory emphasizes the inflexibility
imposed by the high cost of adjusting the production structure by reallocating
installed physical capital. It is
important to realize that similar kinds of inflexibility and high adjustment
costs can come from other resources, particularly labor. Workers often resist seeking employment
outside preferred venues. Because this
source of high unemployment results from high adjustment costs which frustrate
resource allocation and adjustment of the production structure, rather than
from real or nominal wage or price stickiness, this potential cause of
recession, though labor based, should be recognized as Austrian rather than
Keynesian. Mulligan (2002) presents
evidence that labor employment is reallocated over the business cycle in a
manner similar to that predicted by ABC theory for the physical capital it
complements. Hayek (1935:136-139) and
Garrison (1986:440; 1988; 2001:71-73) draw a fundamental distinction between
ordinary changes in time preference and policy-induced changes in interest
rates. Only a decrease in interest rates
caused by credit expansion can drive the business cycle. According to ABC theory, there should be no
cycle if the decrease in interest rates is due to a general lowering of time
preference. Mises (1949:550-566)
develops a similar argument.
3. Qualitative Applications and Earlier Empirics
ABC
theory is unmatched in offering persuasive qualitative explanations of historic
business cycles. This fact by itself
makes a powerful case for the Austrian school, which should be accepted as the
dominant macroeconomic policy paradigm.
Murray
Rothbard's (1963) monumental study of the Great Depression persuasively argues
that credit expansion created an unsustainable boom in the 1920s, and that
government policy frustrated the efforts of economic agents to liquidate
inefficient capital, resulting in a protracted secondary contraction, thus
transforming what would have been a routine recession into the Great Depression
by preventing prompt liquidation of overinvestment. Valuable resources which could have been used
for more productive purposes, and for output more urgently desired by
consumers, instead were tied up in fruitless and counterproductive attempts to
maintain labor employment in the same industries which had already overexpanded
through the malinvestment boom. Focusing
on unorthodox and rarely examined monetary aggregates, Rothbard shows that
inflation and credit expansion continued sporadically well into the 1930s,
effectively preventing any general liquidation of malinvested capital. Rather than facilitate liquidating
malinvestment, easy credit policies generated increased opportunities for
malinvestment. The misallocation of
productive resources was further exacerbated by governmental efforts to restore
and maintain artificially high prices through cartelization.
This
view contrasts markedly with Friedman and Schwartz's (1963) conclusion that the
secondary contraction was caused by the Federal Reserve System's failure to
provide enough liquidity. Using
the standard monetary aggregate that ultimately emerged as M1, Friedman and
Schwartz find that the main problem during the depression was that the money
supply shrank, even though the monetary base grew. Table 1 summarizes some of the evidence cited
by Keynesian, monetarist, and Austrian authors.
It is difficult to avoid the conclusion that the Austrian explanation is
the most encompassing, even though ABC theory focuses on the unsustainable
expansion which precedes a recession.
<<Table
1 about here.>>
The
Austrian perspective can be interpreted as intermediate between the Keynesian
explanation, emphasizing a liquidity trap which made expansionary monetary
policy ineffective, and the monetarist, which criticizes the Fed for
implementing a contractionary policy. The
Austrian school blames the expansionary policy of the 1920s for the onset of
depression, and the reliance on government and central bank policy activism for
transforming what would have been a routine recession into a decade-long
ordeal. The Austrian school goes beyond
the monetarist school in emphasizing the real discoordination and resource
misallocation forced by government and central bank actions, resulting in
persistent and abnormally high unemployment.
O'Driscoll
and Shenoy (1976) present an account of the stagflation of the 1970s in terms
of ABC theory. They note that credit
expansion increases nominal demand at the point the newly-created money is
injected, distorting the price vector and the allocation of resources,
especially of capital which cannot be easily reallocated. Credit expansion always increases consumption
expenditures because any new money results in increased nominal income to some
households. Firms engaging in production
most remote from consumption find resource prices bid up, and resources bid
away, by firms selling directly to consumers.
Unemployment starts in these firms remote from final consumption even as
prices continue to be bid up by continued injections of cheap credit. Garrison (2001) also provides convincing
accounts of both the Great Depression and the stagflation of the 1970s using
the Austrian model.
Carilli
and Dempster (2001) argue that Austrian business cycle theory places undue
reliance on economic agents misperceiving credit expansion as a real increase
in loanable funds. They suggest that
even if rational agents correctly anticipate inflation, agents maximize profits
under uncertainty by taking advantage of the market interest rate whenever it
falls below the underlying rate of time preference. Keeler (2001) used standardized quarterly
data for eight
Powell's
(2002) account of the Japanese recession of the 1990s is especially noteworthy
because he focuses on exactly how expansionary monetary and fiscal policy
recommended to spur recovery, actually lengthened and deepened
In
marked contrast to orthodox neoclassical and Keynesian accounts of the business
cycle, Austrian business cycle theory presents a consistent and coherent
explanation of the causes and propagation mechanisms of the business
cycle. Though more typically qualitative
than quantitative, the explanatory successes of Austrian business cycle theory
have proved robust over an impressive time period and range of specific
applications. This remarkable success
makes it even more puzzling that ABC theory has not been enthusiastically
embraced by non-Austrians, and that it has yet to emerge as the dominant macroeconomic
policy paradigm.
4. Data
This
section documents the data used for econometric estimation and motivates the
choice of data. Annualized personal
consumption expenditures and its chain-type price index are observed monthly
for January 1959 to March 2003 and reported by the U.S. Department of Commerce
Bureau of Economic Analysis. The price
index was used to obtain real personal consumption expenditures, which was then
put in natural logarithms. This is the
measure of real consumable output.
Alternative
output measures present special difficulties.
Most national income and product account output measures, such as gross
domestic product (GDP), are only observed quarterly. Often, the
monthly-observed index of industrial production is used to proxy GDP. These broader output measures include
investment and government purchases.
They are less appropriate from an Austrian perspective because ABC theory
purports to explain fluctuations in real consumable output. It would be especially interesting to
estimate the relationship between interest rates and real private investment
spending, but investment is only observed quarterly.
One
difficulty which cannot be avoided is that in the Austrian view, the real value
of consumable output is not the objective and observable exchange value
captured in real consumption expenditures, but the subjective use value
extracted by each consumer. This value
is inherently unobservable and disaggregated.
Such fundamental issues of methodology and philosophy help explain why
there have been so few econometric analyses of Austrian theories.
Interest
data are provided by the Federal Reserve Bank of
mt
= (1 + at)1/12 – 1.
The
term spread was found to be a stationary process (see section 6.a.), and thus
could not have a stable, cointegrated relationship with a nonstationary process
like real consumable output. To overcome
this problem, the cumulative sum of the term spread (r) was computed and used
in estimation:
rt
= {Pi=1t(1 + mn)}
– 1.
The
cumulative term spread can be interpreted as the real return over time, which
is then put in natural logarithms. All
data are from the Federal Reserve Bank of St. Louis Federal Reserve Economic
Data (FRED-II) website.
5. The Error-correction Methodology
This
paper proposes the error-correction model as an econometric methodology
especially amenable to interpretation by the Austrian school. Error-correction models provide estimates of
both a structural or equilibrium process toward which adjustment is generally
effected, and the error-correction or disequilibrium adjustment process through
which adjustment is made toward the hypothesized equilibrium. Even if one rejects the reality of any
hypothesized equilibrium, estimates of the disequilibrium adjustment process
still warrant interest.
The
error correction model consists of two parts, a structural equation which
defines the equilibrium process, and a disequilibrium adjustment process. If this equation were estimated by ordinary
least squares or any other econometric technique, the residual of the
structural equation would define the extent of disequilibrium in any given time
period.
For
consumption, the structural equation capturing the long-run relationship
between consumption and the cumulative real interest yield is:
Ct
= ARtbEt
where A is a scaling
constant, b is a weighting exponent, and E is a multiplicative residual or
error. Putting this relationship in
logarithms yields:
ct
= a + brt + et
where
c and r are the natural logarithms of consumption and the cumulative term spread[2],
and the vector error correction model is:
Dct = Q(ct-1 - a - brt-1)
+Dct-1 +Dct-2 + Dct-3 …+Drt-1 +Drt-2 + Drt-3 …+ut
Drt = Y(ct-1 - a - brt-1)
+Dct-1 +Dct-2 + Dct-3 …+Drt-1 +Drt-2 + Drt-3 …+vt
Note
the expression in parentheses is the lagged residual from the structural
equation, and thus could be represented simply by et-1. This is
the error which the disequilibrium adjustment process of the error correction
model attempts to explain. The
upper-case Greek letters are the structural adjustment or disequilibrium
adjustment terms, which weight the error-correction processes and so indicate
the importance of the past changes in the explanatory variables in effecting
adjustment toward the hypothesized equilibrium.
The equilibrium represented by the structural equation is generally
never realized, and if realized, is not persistent. If equilibrium is ever reached, that is
represented by a zero residual in the structural equation for those
observations. Whenever the residual is
non-zero, that is, whenever the system is in disequilibrium, which generally
will be for virtually every observation, the non-zero residual in period t
results in an adjustment back toward equilibrium in period t+1, represented by
the error-correction processes. The
error-correction processes can be thought of as indicating how the data
processes can best be represented as adjusting to maintain the long-run
equilibrium.
Conventional
inference is valid in an error-correction model even when the structural
variables are nonstationary, provided the residuals are white-noise processes
with no serial correlation. It is
generally assumed that adding a sufficient number of lagged difference terms in
the disequilibrium adjustment process is always sufficient to guarantee
white-noise errors.
6. The Vector Error-correction Model
This
section presents and interprets empirical estimates based on a simple parameterization
of Austrian business cycle theory. In
the subjectivist theory of a capital-using economy, entrepreneurial planners
act as the subjects of productive activities, creating real consumable output
as the object (Garrison 1985:164-165; 2001:15). Interest rates facilitate
intertemporal coordination of productive resources by clearing the loanable
funds market (Garrison 1986:440; 2001:39).
In this regard disequilibrium interest rates play the same role as
prices in signaling opportunities for entrepreneurial discovery (Kirzner
1984a:146; 1984b:160-161; 1997), and individual entrepreneurs respond by
maintaining the production structure, that is, they adjust it by reallocating
resources.
a. Unit Root and Cointegration Tests
Most
macroeconomic time series display an increasing trend, and unit root tests were
developed to identify this characteristic.
Stationary time series are said to have zero roots or be integrated of
order zero [I(0)]. Non-stationary series
may have a unit root or be first-order integrated [I(1)]. Unit root series become I(0) when
first-differenced. Regressions estimated
with non-stationary data will not have the white-noise residuals needed for
valid inference. The regression could be
estimated in first-differences, but then any long-term information carried by
the levels of the variables is lost.
Error-correction models overcome this difficulty by estimating a regression
in first-differences augmented by error-correction terms, the lagged
differences between the actual and estimated value of the left-hand-side
variable, collectively referred to as the error-correction process, also called
the disequilibrium adjustment process.
The coefficients on the first-differenced variables constitute the
cointegrating vector or structural relationship. A sufficient number of lagged
error-correction terms are added to guarantee white-noise errors and valid
inference (Davidson and McKinnon 1993:720-730, Kennedy 1998:266-270).
The
Johansen-Juselius (1990) procedure was used to identify stable, long-term
relationships between real consumable output and the interest rate term
spread. Table 2 reports augmented
Dickey-Fuller (1979) and Phillips-Perron (1988) unit-root tests for each
variable. Because unlike consumption
expenditures, interest rates do not generally rise as the economy grows, the
term spread would be expected to be I(0) a priori. This result was obtained empirically here
with the augmented Dickey-Fuller test, in contrast to Mulligan (2002), who
found interest rates I(1) with the Phillips-Perron test. Although the Phillips-Perron test indicates
both the term yield and the cumulative term yield are I(0), following the Dickey-Fuller
results, the cumulative term yield was treated as I(1).
<<Table 2
about here.>>
An
I(1) process like consumption cannot be cointegrated with an I(0) process like
the term spread. One way around this
difficulty would be to difference consumption, yielding an I(0) process. Almost equivalently, the cumulative sum of
the term spread could be generated.
Though these two procedures are numerically nearly identical, cumulative
summing the term spread avoids losing one observation and one degree of freedom
in estimation, and that was the procedure followed here. Unit root tests confirm the cumulative term
spread is I(1). The null hypothesis of a
unit root is always rejected for the first-differenced series, demonstrating
both variables are integrated of order one [I(1)] and not of higher order.
Table
3 reports Johansen-Juselius tests for cointegration. Results of the trace test, a likelihood
ratio, indicate a stable, cointegrated relationship between real consumable
output and the cumulative yield spread.
Stronger evidence for cointegration was found when the model was
specified without a constant in the structural equation, but the intercept was
left in to avoid imposing an unrealistic restriction. This determined the specification of the vector
error-correction model.
<<Table 3
about here.>>
Because
the two variables in the model are cointegrated, the ordinary least squares
estimate of the structural relationship has the property of
superconsistency. The OLS estimate is
presented in table 4, and it can be seen that OLS provides an estimate of the
structural relationship or cointegrating equation fairly consistent with that
provided by the error-correction model (Table 5.) The OLS estimate also allows for a test of
the hypothesis that a lower interest rate accompanies a permanently lowering of
the level of real consumable output, the key assertion of Austrian business
cycle theory. The adjusted R square is 97%. The intercept and coefficient on the
cumulative term spread are both positive and significant. Coefficient values of 6.862 for the intercept
and 0.162 for the slope indicate that a one percent increase in interest rates
permanently raises consumption expenditure by 955.3 billion chained 1996 dollars
each month the higher interest rate persists.[3]
<<Table 4 about
here.>>
Perhaps
more revealingly, a one-percent decrease in the cumulative term spread,
such as results from policy induced monetary expansion, has on average decreased
real consumable output over the long run by the same amount. The results of the t-test on the cumulative
term spread provide strong empirical confirmation of Austrian business cycle
theory. This amount is more than great
enough to account for any historic recession. Further, the output measure used here, real consumption
expenditures, comprises only approximately 70% of GDP, thus any impact on real consumption
implies a somewhat greater impact on total real output.
b. The Cointegration Space
The
estimate of the vector error correction model (VECM) is reported in table 5. To facilitate interpretation, the VECM is
normalized with respect to and solved for consumption. Estimated coefficients of the cointegrating
equation are similar in sign and magnitude to those found by OLS. The VECM intercept and slope coefficients
7.120 and 0.136, indicating a one-percent decrease in the cumulative term
spread decreased real consumable output by approximately 1,236 billion 1996
dollars for every month. This is significantly
greater than the amount indicated by OLS, but the two estimates are reasonably
consistent. The t-test on the VECM
estimate of the structural equation provides further evidence in support of
Austrian business cycle theory's key assertion that lowering the interest rate
lowers real consumable output over the long run. The coefficients on the ninety-six lagged
difference terms are not reported, partly due to space limitations, and also
because individual coefficient estimates hold limited interest. The implications of the disequilibrium
adjustment process can be inferred from the variance decomposition and impulse
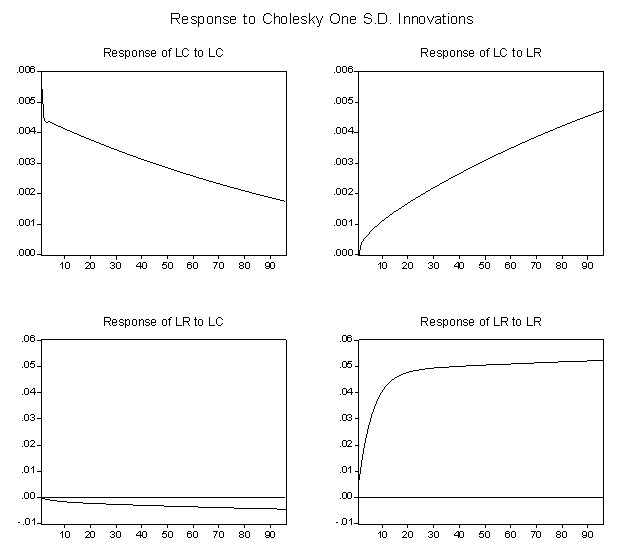
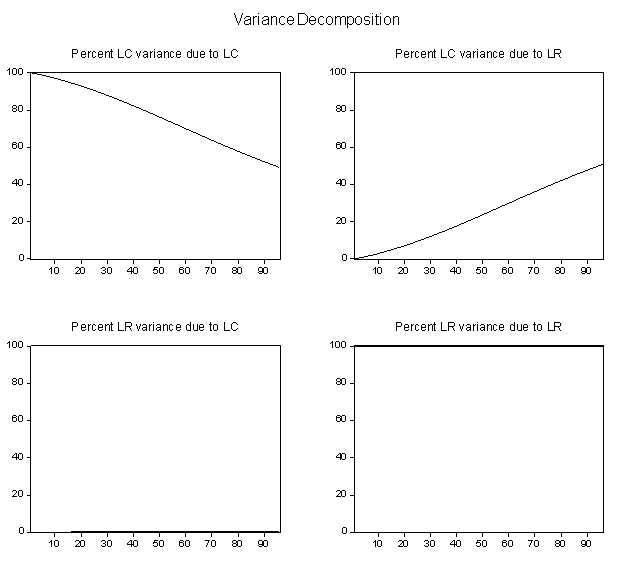
response graphs (Figures 1 and 2).
<<Table 5
about here.>>
The
adjusted R-square for the disequilibrium adjustment process is very high (92%)
for the cumulative term spread disequilibrium adjustment process, but very low
(16%) for the real consumable output process.
Ideally a model with high explanatory power would explain the adjustment
process for both consumption and interest rates, but it is a significant
triumph for ABC theory that the adjustment process appears to work primarily
through the interest rate. The feedback
loop through consumption is relatively weak.
In spite of the low R-square, the disequilibrium adjustment term in
consumption [Q] is negative and significant, indicating that consumption adjusts
downward whenever consumption exceeded the fitted (a + brt-1) in the previous
month, or in other words, whenever ct-1 > a - brt-1,
or whenever et-1 was positive.
The disequilibrium adjustment term in the term spread [Y] is positive but not
significant.
The
specification of the disequilibrium adjustment process includes only lagged
first-differences of both consumption and the cumulative term spread, one
through ninety-six, eight years of lagged differences. This lag specification was arrived at through
Wald tests for lag exclusion. A full
year of lagged differences were retained as long as any one of the twelve was
statistically significant.[4] In addition to hypothesis tests, appeal
could be made to a priori, theoretical, or observational-empirical
considerations in setting the lag length.
The median length of a recession is somewhat less than two years, but
the median length of an expansion may be as long as ten years. One approach would be to average the two
figures to ensure capturing most of the dynamics in the disequilibrium
adjustment process. However, the average
expansion generally cannot last so long if it is characterized by
policy-induced credit expansion. The
complete dynamics of the business cycle may be captured with four to five years
of lagged differences. This would be the
case if a recession always results after so many years of credit expansion, and
if the recessions are always shorter than the expansions. This study, in contrast, errs on the side of
caution and statistical formalism by including the longer lag structure.
Validity
of the error-correction specification depends on cointegration among the
variables in the model and white-noise characteristics of the residuals. Jarque-Bera (1980) tests of normality of the
residuals are reported in Table 6.
Unfortunately these results strongly suggest the residual series are
non-normal. It should be emphasized,
however, that normality is a sufficient, rather than a necessary, condition for
valid VECM estimates. The
Johansen-Juselius procedure estimates the VECM by maximum likelihood, imposing
the most nearly normal character possible on the residuals. In the absence of a clear finding of normal
residuals, appeal has to be made to the very similar coefficients of the
superconsistent OLS estimate. Even when
96 lagged differences, representing eight years, were added to the model, the
Jarque-Bera test yielded a result of non-normality.
<<Table 6 about
here.>>
Non-normal
residuals can be interpreted as evidence of specification error, and from the
perspective of the Austrian school, specification error is necessarily present
in all econometric models. The measure
of real consumable output is not the subjective use value of the output
delivered to consumers, and the real interest rate measure is not the idealized
interest rate hypothesized by Hayek and Mises (Garrison 1985:169-170; 2001:50;
Rothbard 1970:321-323). Thus, Austrian
methodological arguments suggest an a priori expectation of unavoidable
misspecification and measurement error in any econometric empirical work.
c. Granger Causality Tests
Granger causality tests (Granger 1969)
are presented in table 7, indicating rejection of the null hypotheses that the ninety-six
lagged differences of consumption and the cumulative yield spread can be
deleted from the system. Thus both
variables are endogenous with respect to one another. This is found both in the context of the VECM
and with a generalized, non-VECM-specific test.
Granger causality tests depend on the maintained hypothesis that all
relevant variables have been included in the VECM (Davidson and MacKinnon 1993:686). Although ABC theory asserts that real consumable
output depends on the stability of the money supply and the maintenance of an
appropriate, sustainable interest rate, it might reasonably be questioned
whether all relevant variables have been included, especially in light of the
Austrian school’s methodological criticisms of output and interest rate
measures. Orthodox neoclassical and Keynesian
economists could contribute additional reasons to suspect omitted
variables. The Granger causality tests
should be viewed as inherently context dependent.
<<Table 7 about here.>>
d. Impulse Response Functions
Graphs
of the impulse response functions are presented in figure 2. The upper-right-hand graph is the one of
interest for Austrian business cycle theory.
It indicates that over the period studied, a one standard-deviation
increase in the term spread has resulted, on average, in an upward adjustment
of approximately .004 in the logarithm of consumption, equivalent to 1.004
billion 1996 dollars after eight years or 96 months. A one standard deviation decrease in
the yield spread decreased real consumable output by an equivalent
amount, on average.
<<Figure 2 about
here.>>
e. Variance Decomposition Functions
Graphs
of the variance decomposition functions are presented in figure 3. Again, the upper-right-hand graph is the one
of interest for Austrian business cycle theory.
This graph indicates that after eight years or 96 months, nearly 45-50%
of the variance in real consumption expenditures has been attributable to
variation in the cumulative term spread, over the period studied. Interestingly, no variation seems to be
transmitted from consumption to the interest rate.
<<Figure 3 about
here.>>
7. Conclusion
This
paper presents evidence of cointegration between real consumable output and the
cumulative interest rate term spread.
This finding implies a close relationship between the change in real
consumable output and the term spread, as well as the real interest rate it
proxies. Austrian business cycle theory
is applied to interpret these empirical regularities. A simple vector error-correction model is
specified and presented, and demonstrated to have a great deal of explanatory
power over 1959-2003 historical data.
Cointegration
analysis identifies a stable long-term relationship between consumption and the
cumulative term spread. The
cointegrating vector constitutes a dynamic equilibrium entrepreneurial planners
have generally effected adjustment toward during the 1959-2003 observation
period. This equilibrium is not
necessarily ever realized. The market
process consists of entrepreneurial planners effecting adjustment toward a
dynamic equilibrium they continuously redefine.
The prevailing term structure of interest rates determines resource
allocation among early, middle, or late stages of production, allocating
resources and production in accordance with consumers' time preference and
available investment alternatives.
Estimates of a stable long-run relationship using
If
every month the real interest rate falls 100 basis points below its
hypothesized market-clearing rate costs us approximately one trillion dollars
worth of real consumable output, it might be assumed that ABC theory prescribes
raising the interest rate as high as possible.
The reason this interpretation is untenable is that the data include
many periods where interest rates were kept inappropriately low, but none where
they were inappropriately high. Because
policy imperatives impose this asymmetric character on the data, interpretation
does not allow the conclusion that monetary policy works symmetrically in both
directions.
ABC
theory is founded on the concept of a sustainable, market-determined interest
rate, and predicts negative consequences when that equilibrium is persistently
disturbed. Economists and laypeople are
well aware of these consequences: the periodic high unemployment associated
with the business cycle. The policy
prescriptions of the Austrian school are unmistakable: first, never disturb the
interest rate with credit expansion or monetary inflation, and second, after
the first policy prescription has been violated, never interfere with
entrepreneurial planners' efforts to liquidate suboptimal production plans as
rapidly as possible. As long as
economists and policy makers believe the business cycle can be avoided through
the activism of charismatic central bankers, recessions will be inevitable.
Acknowledgement
Financial
support in the form of a Visiting Research Fellowship from the American
Institute for Economic Research, is gratefully acknowledged. Thanks are due to Scott Beaulier,
Notes